Question

Постройте график функции y=9x+1/9x^2+x и определите при каких значениях k, прямая y=kx имеет с графиком ровно одну общую точку.

Answer 1

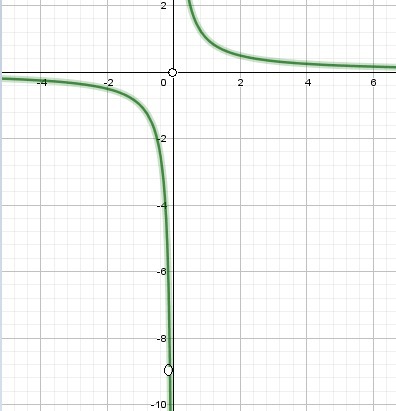
Область определения функции: функция существует, если $9x^2+xne 0$
$x_1ne 0\ x_2ne- frac{1}{9}$

Упростим функцию

$y= dfrac{9x+1}{9x^2+x}= dfrac{9x+1}{x(9x+1)}= dfrac{1}{x}$ - гипербола

y =kx - прямая, которая проходит через начало координат. И очевидно, что прямая будет пересекаться с графиком y=1/x в двух точках, кроме x=0 и x=-1/9

Если x = -1/9, то y = -9

y = kx  подставив данные, получим -9 = -k/9  откуда  k=81

ОТВЕТ: k=81

Answer 2

ДАНО
$Y= frac{9x}{9x^2+x}$ - функция
Y = k*x - прямая
НАЙТИ
k = ? - одна точка пересечения с функцией.
РЕШЕНИЕ
Немного подумав находим "лазейку" в функции, что бы прямая прошла не пересекая функции.
1) Находим область определения функции. Не допускается деление на 0 в знаменателе.
9*x² + x = x*(x + 1/9) ≠ 0.
х ≠0 и х ≠ - 1/9.
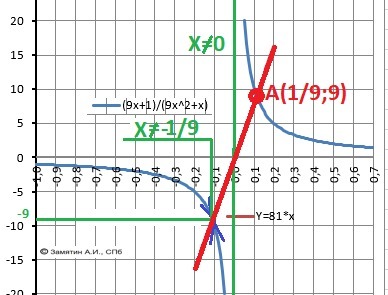
Dx - X∈(-∞;-1/9)∪(-1/9;0)∪(0;+∞).
Вот и появилась "выколотая" точка на левой ветви графика функции.
2) Находим координаты этой несуществующей  точки графика.. Вычисляем предел функции при Х = - 1/9.
lim(-1/9)Y(x) = - 9 или Z(-1/9;-9) - координата "дырки" в графике.
 3) Проводим прямую по уравнению Y = k*x через точку Z и находим коэффициент наклона  -  k
k = ΔY/ΔX = -9 : (- 1/9) = 81 - параметр - ОТВЕТ
ДОПОЛНИТЕЛЬНО
Единственная точка пересечения - А(1/9;9).
Уравнение X = 0 -не может быть - функция не определена.
Уравнение У = 0 - значение функции не определено.