Question

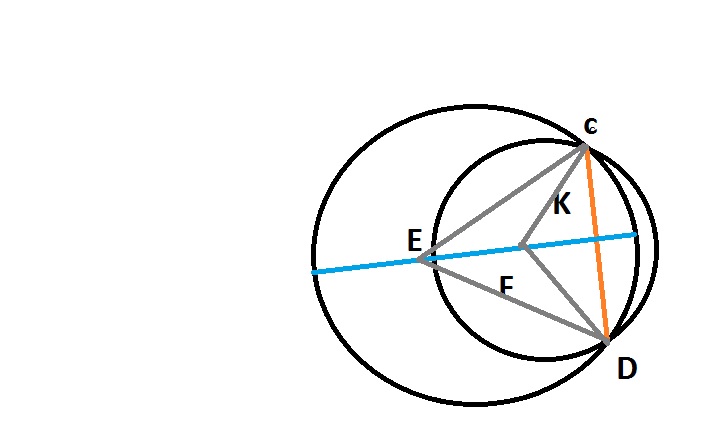
Окружности с центрами в точках E и F пересекаются в точках C и D, причем точки E и F лежат по одну сторону от прямой CD. Докажите, что CD перпендикулярно EF.

Answer 1

Всё легко.Перечерти мой рисунок.
Далее рассматриваем тр.-ник  ECD.В нём EC=CD(следовательно треугольник равнобедренный) и проведён диаметр EK.Нам нужно доказать,что он (EK) перпендикулярен CD.Для этого строим FC и FD,опять равнобедренный треугольник FCD,где FC=FD.Из равенства углов ECD=CDE и FCD=FDC получаем,что ECK=KDE.Выходит,что треугольник ECF и EDF равны по двум сторонам и двум углам между ними.Из этого следует,что угол CEK=DEK.
Теперь вернёмся к треугольнику ECD.В нём EK-биссектрисса,а значит и медиана.Отсюда следует,что CK=KD.Теорема доказана.
P.s.Ты с Дальнего Востока?

Answer 2

А как доказать, что треугольники равнобедренные?

Answer 3

В доказательстве не было объяснено, откуда взялось, что стороны равны

Answer 4

это вроде радиусы большей окр