Question

Най­ди­те ве­ли­чи­ну (в гра­ду­сах) впи­сан­но­го угла α, опи­ра­ю­ще­го­ся на хорду  AB, рав­ную ра­ди­у­су окруж­но­сти.

Answer 1

Пусть AB — рассматриваемая хорда, O — центр окружности.
Доп.построение: OA и OB — радиусы окружности.
Получим:
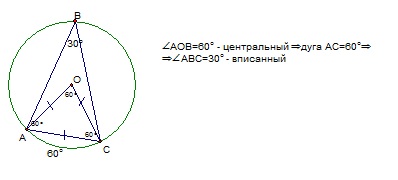
1)Рассмотрим треугольник ABO. В нем AB = OA = OB — все стороны равны радиусу окружности т.к треугольник ABO — равносторонний, и все углы в нем по 60°.
2)Пусть M — вершина вписанного угла. Поскольку углы O и M опираются на одну и ту же дугу AB, вписанный угол M в 2 раза меньше центрального угла O. 
Имеем:M = O : 2 = 60 : 2 = 30