Предмет: Геометрия,
автор: viporazgaliev2
1. Неравенство треугольника (доказать).
Ответы
Автор ответа:
0
Теореме о неравенстве треугольника:
Длина любой стороны треугольника меньше суммы двух других его сторон.
Пусть АС - большая сторона треугольника.
Докажем, что АС < AB + BC.
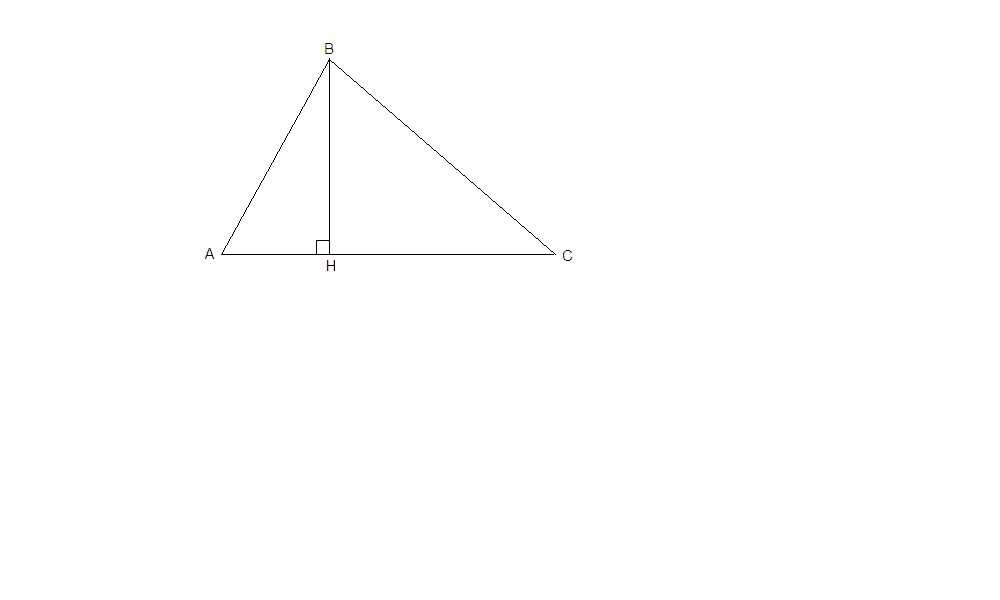
Опустим высоту ВН на сторону АС.
В треугольнике напротив большего угла лежит большая сторона. В прямоугольном треугольнике прямой угол - самый большой, напротив него лежит гипотенуза, значит катет всегда меньше гипотенузы.
ΔАВН: АН < AB
ΔCBH: CH < BC, складываем неравенства и получаем:
АН + СН < AB + BC или
AC < AB + BC.
Так как теорема доказана для большей стороны, для двух других сторон она очевидно верна.
Длина любой стороны треугольника меньше суммы двух других его сторон.
Пусть АС - большая сторона треугольника.
Докажем, что АС < AB + BC.
Опустим высоту ВН на сторону АС.
В треугольнике напротив большего угла лежит большая сторона. В прямоугольном треугольнике прямой угол - самый большой, напротив него лежит гипотенуза, значит катет всегда меньше гипотенузы.
ΔАВН: АН < AB
ΔCBH: CH < BC, складываем неравенства и получаем:
АН + СН < AB + BC или
AC < AB + BC.
Так как теорема доказана для большей стороны, для двух других сторон она очевидно верна.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Литература,
автор: aruzanabdulaeva24
Предмет: Алгебра,
автор: alexsstepo
Предмет: Алгебра,
автор: asan2001