Question

найдите радиус окружности, описанной около правильного треугольника, площадь которого 3 корня из 3

Answer 1

Если в окружность вписан ПРАВИЛЬНЫЙ треугольник, то его центр будет совпадать с центром описанной около него окружности.
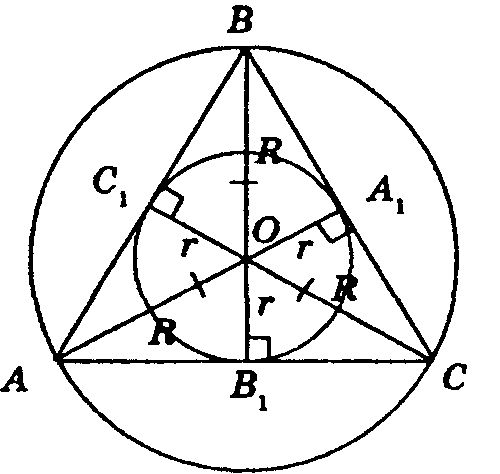
Нам дан ΔАВС с высотами АА₁, ВВ₁ и СС₁ и окр. с центром в точке О. SΔ=3√3.
OB=OC=OA=R
Пусть AB=BC=CA=X, тогда СС₁=$frac{ sqrt{3} }{2}x$
CO:OC₁ как 2:1, ⇒ $R= frac{ sqrt{3}}{2}x* frac{2}{3}= frac{ sqrt{3}}{3}x$
$S= frac{1}{2}*CC_{1}*AB= 3sqrt{3} \ frac{1}{2}* frac{ sqrt{3}}{2}x*x= 3sqrt{3} \ frac{ sqrt{3}}{4} x^{2}= 3sqrt{3} \ x^{2}=12 \ x= 2sqrt{3}$
То есть AB=BC=CA=2√3
$R= frac{ sqrt{3}}{3}x=frac{ sqrt{3}}{3}* 2sqrt{3}= frac{6}{3}=2$
Ответ: 2.