Question

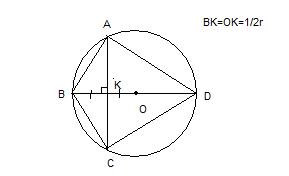
отрезок BD- диаметр окружности с центром О.Хорда АС делит пополам радиус ОВ и перпендикулярна к нему .Найдите углы четырёхугольника ABCD и градусные меры дуг AB,BC,CD,AD.

Answer 1

Т.к. вписанные углы BAD и BCD опираются на полуокружности, то они - прямые. Треугольники BAD и BCD - прямоугольные. Рассмотрим треуг-ик BAD. АК здесь - высота. Для катета АВ можно записать:
AB=√BK*BD=√1/2r*2r=√r²=r
BD=2r, значит АВ = 1/2 BD.
Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°. Значит, <ADB=30°.
Зная, что сумма острых углов прямоугольного треугольника равна 90°, находим угол ABD:
<ABD=90-<ADB=90-30=60°
В прямоугольном треугольнике BCD для катета ВС можно точно также записать, что
BC=√BK*BD=√1/2r*2r=√r²=r
Треугольники BAD и BCD, таким образом, равны по гипотенузе (она у них общая BD) и катетам АВ и ВС. Значит
<ABC=2*<ABD=2*60=120°
<ADC=2*<ADB=2*30=60°
Вписанные равные углы ADB и СDB опираются на равные дуги АВ и ВС, углы равны половине этих дуг. Значит:
АВ=ВС=30*2=60°
Вписанные равные углы ABD и CBD опираются на равные дуги AD и CD, углы равны половине этих дуг. Значит:
AD=CD=60*2=120°