Предмет: Алгебра,
автор: Катя2013март
исследуйте функцию на монотонность и экстремумы
надо срочно
Приложения:
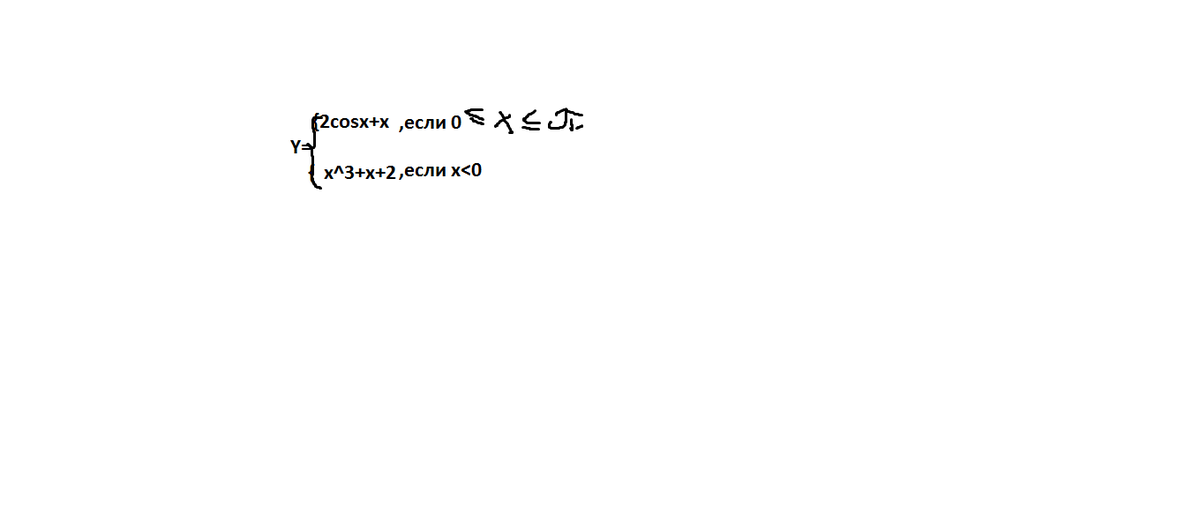
Ответы
Автор ответа:
0
1)  , x∈[0;pi]
, x∈[0;pi]

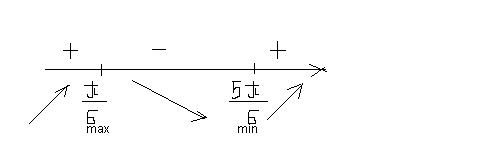
Наносим на числовую ось, расставляем знаки (рис.1). Знаки монотонности расставлены, экстремумы подписаны.
2) x<0
x<0

Приравнивая к нулю, получаем, что x принадлежит пустому множеству, а f'(x) всегда больше нуля, значит, функция возрастает при x<0, а экстремумов на данном промежутке нет.
Наносим на числовую ось, расставляем знаки (рис.1). Знаки монотонности расставлены, экстремумы подписаны.
2)
Приравнивая к нулю, получаем, что x принадлежит пустому множеству, а f'(x) всегда больше нуля, значит, функция возрастает при x<0, а экстремумов на данном промежутке нет.
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: karinazhaukenova
Предмет: Математика,
автор: Battlewith
Предмет: Математика,
автор: laleksander196
Предмет: Алгебра,
автор: mucky15