Предмет: Алгебра,
автор: Аноним
система уравнений))))))))))))
Приложения:
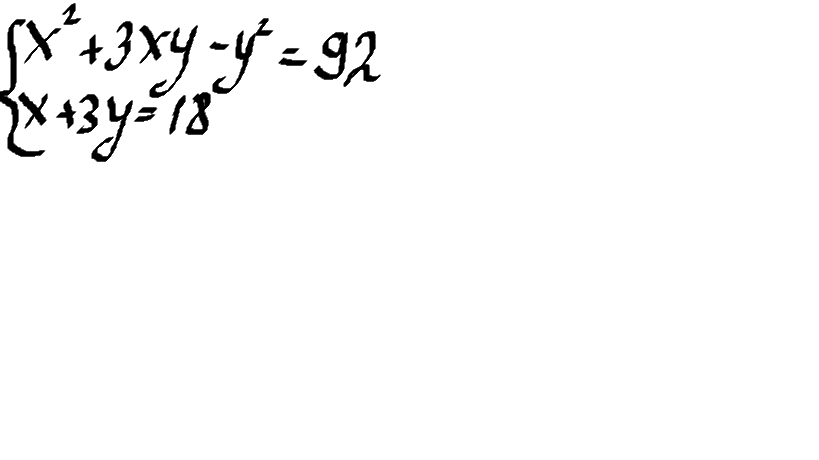
Ответы
Автор ответа:
0
Ответ (192;-58) (6;4)
Автор ответа:
0
Из 2-ого уравнения находим х: (x = 18 - 3y) и его значение подставляем в 1-ое уравнение и решаем его:
( 18- 3у)^2 + 3(18-3y)*y - y^2 = 92
324 - 108y + 9y^2 + (54 - 9y) * y - y^2 = 92
324 - 108у +9у^2 + 54y - 9y^2 - y^2 - 92 = 0
-y^2 - 54y + 232 = 0
y ^2 + 54y - 232 = 0
D = 2916 - 4 ( - 232) = 2916 + 928 = 3844; YD = 62
y1 = (-54 + 62) / 2 = 4
y2 = (-54 - 62) / 2 = - 58
Подставляем найденные у во 2-ое уравнение и решаем его:
х + 3у = 18
х1 = 18 - 3у1 х2 = 18 - 3у2
х1 = 18 -12 х2 = 18 -3(-58)
х1 = 6 х2 = 18 + 174
х2 = 192
Ответ: х1 = 6 х2 = 192
у1 = 4 у2 = - 58
( 18- 3у)^2 + 3(18-3y)*y - y^2 = 92
324 - 108y + 9y^2 + (54 - 9y) * y - y^2 = 92
324 - 108у +9у^2 + 54y - 9y^2 - y^2 - 92 = 0
-y^2 - 54y + 232 = 0
y ^2 + 54y - 232 = 0
D = 2916 - 4 ( - 232) = 2916 + 928 = 3844; YD = 62
y1 = (-54 + 62) / 2 = 4
y2 = (-54 - 62) / 2 = - 58
Подставляем найденные у во 2-ое уравнение и решаем его:
х + 3у = 18
х1 = 18 - 3у1 х2 = 18 - 3у2
х1 = 18 -12 х2 = 18 -3(-58)
х1 = 6 х2 = 18 + 174
х2 = 192
Ответ: х1 = 6 х2 = 192
у1 = 4 у2 = - 58
Похожие вопросы
Предмет: Окружающий мир,
автор: zhskbevaa
Предмет: Литература,
автор: davidxiomi2000
Предмет: Геометрия,
автор: skobel24
Предмет: Геометрия,
автор: Аноним
Предмет: Физика,
автор: li2405