Предмет: Алгебра,
автор: piratik45
Найдите S * n, где S - сумма корней уравнения, n - количество корней
Приложения:
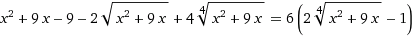
Ответы
Автор ответа:
0
по теореме Виета сумма корней равна
Автор ответа:
0
давайте скажу лучше , сам метод такого разложения , так как у вас уравнение четвертой степени то есть старшая степень у вас 4 , значить если у вас это выражение разложится на множители то в таком виде (x^2+bx+c)(x^2+dx+e) . и можно добавить такое условие к a,c они в произведений должны давать всегда 3 , так как у вас оно равно 3 , то получим систему уравнений если умножим оба множителя и приравняем соответсвтующие коэффициенты исходным
Автор ответа:
0
Да, логично. Ещё раз благодарю Вас..
Похожие вопросы
Предмет: География,
автор: nikitenkoekaterina21
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: sashdhkaya97
Предмет: Математика,
автор: alekseirysev