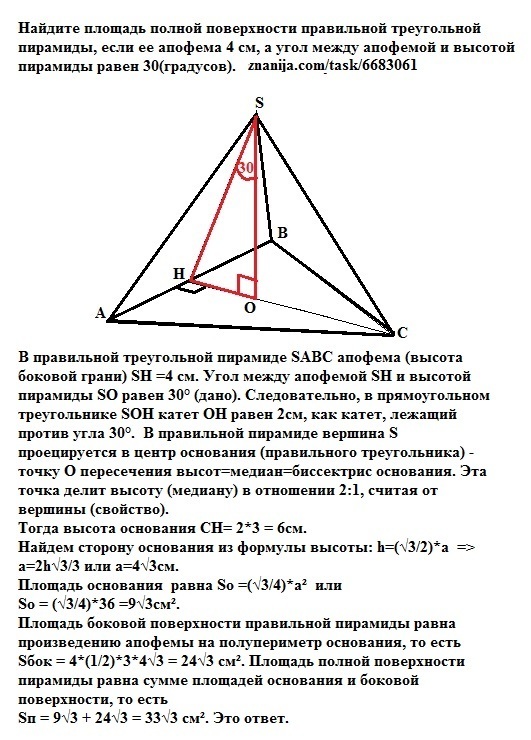
Найдите площадь полной поверхности правильной треугольной пирамиды, если ее апофема 4 см, а угол между апофемой и высотой пирамиды равен 30(градусов).
Ответы
В правильной треугольной пирамиде SABC апофема (высота боковой грани) SH =4 см. Угол между апофемой SH и высотой пирамиды SO равен 30° (дано). Следовательно, в прямоугольном треугольнике SOH катет ОН равен 2см, как катет, лежащий против угла 30°. В правильной пирамиде вершина S проецируется в центр основания (правильного треугольника) - точку О пересечения высот=медиан=биссектрис основания. Эта точка делит высоту (медиану) в отношении 2:1, считая от вершины (свойство).
Тогда высота основания СН= 2*3 = 6см.
Найдем сторону основания из формулы высоты: h=(√3/2)*a => a=2h√3/3 или а=4√3см.
Площадь основания равна So =(√3/4)*a² или
So = (√3/4)*36 =9√3см².
Площадь боковой поверхности правильной пирамиды равна произведению апофемы на полупериметр основания, то есть
Sбок = 4*(1/2)*3*4√3 = 24√3 см². Площадь полной поверхности пирамиды равна сумме площадей основания и боковой поверхности, то есть
Sп = 9√3 + 24√3 = 33√3 см². Это ответ.