Предмет: Геометрия,
автор: НеЗнаюМатематику0
Ребяты, решите, пожалуйста.
Подробно и правильно, если не сложно, конечно.
(А вам же не сложно, это только я такой идиот :С )
Приложения:
Ответы
Автор ответа:
0
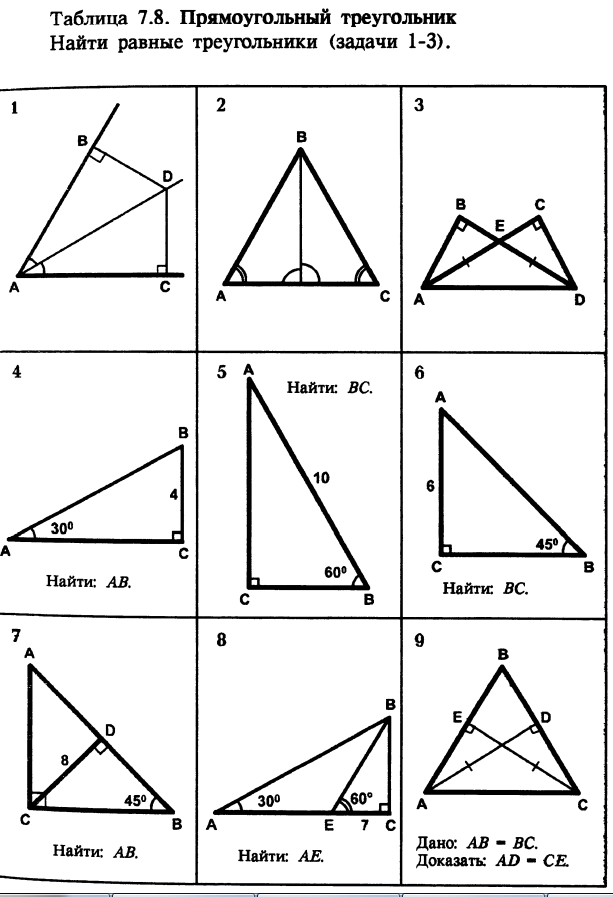
1. Пользуемся одним из признаков равенства прямоугольных треуг-ов: если гипотенуза и острый угол одного прямоугольного треуг-ка соответственно равны гипотенузе и острому углу другого, то такие треугольники равны. В нашем случае: AD - общая гипотенуза, <BAD=<CAD по условию.
2. Поскольку углы А и С равны по условию, треугольник АВС - равнобедренный и АВ=ВС. Из точки В проведен отрезок к основанию АС. Поставим там точку Н, например (я делать этого не буду, обозначь на рисунке точку сам). В треугольниках АВН и НВС по 2 одинаковых угла: <A=<C, <AHB=<СHВ. Исходя из того, что сумма углов треугольника равна 180 градусов, углы АВН и СВН также будут равны. Получаем, что треугольники АНВ и СНВ равны по второму признаку равенства треугольников: сторона и два прилежащих к ней угла одного треугольника соотвественно равна стороне и двум прилежащим к ней углам другого треугольника: АВ=ВС, <A=<C, <ABH=<CBH.
3. Треугольник AED равнобедренный по условию, значит углы EAD и EDA при его основании равны. Получается, что в прямоугольных треугольниках ACD и ABD гипотенуза AD - общая, а острые углы EAD и EDA равны. Следовательно, треугольники ACD и ABD равны по одному из признаков равенства прямоугольных треугольников: гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого.
Прямоугольные треугольники АВЕ и DCE также равны по гипотенузе и катету: АЕ=ED по условию (это гипотенузы), АВ=CD (катеты). Почему эти катеты равны, доказано выше (прямоугольные ACD и ABD равны между собой).
4. Зная, что в прямоугольном треугольнике катет ВС, лежащий против угла в 30 градусов, равен половине гипотенузы АВ, находим АВ:
ВС= АВ : 2, отсюда АВ = ВС * 2 = 4*2=8
5. Зная, что сумма острых углов прямоугольного треугольника равна 90 градусов, находим угол А:
<A=90-<B=90-60=30°
Катет ВС в прямоугольном треугольнике лежит против угла А в 30°, значит, он равен половине гипотенузы АВ:
ВС=АВ:2=10:2=5
6. Зная, что сумма острых углов прямоугольного треуг-ка равна 90°, находим угол А:
<A=90-<B=90-45=45°
Таким образом, треугольник АВС является равнобедренным, поскольку углы при его основании АВ равны. Значит
ВС=АС=6
7. Рассмотрим прямоугольный треуг-ик CDB. Зная, что сумма острых углов прямоугольного треугольника равна 90°, находим угол DCB:
<DCB=90-<B=90-45=45°
Таким образом, получаем, что треуг-ик CDB является равнобедренным, т.к. углы при его основании ВС равны. Значит
CD=BD=8
В прямоугольном треуг-ке АВС угол А равен 90-<B=90-45=45°, он также равнобедренный. Высота CD, проведенная в равнобедренном треугольнике к его основанию, является также и медианой. Значит
BD=AD=8, AB=8+8=16
8. Рассмотрим прямоугольный треугольник ВСЕ. Зная, что сумма острых углов прямоугольного треуг-ка равна 90°, находим угол СВЕ:
<CBE=90-<BEC=90-60=30°
В прямоугольном треугольнике катет, лежащий против угла в 30°, равен половине гипотенузы, значит
ЕС=ВЕ:2, отсюда ВЕ=2*ЕС=2*7=14
В треугольнике АВЕ угол АЕВ равен 180-<BEC=180-60=120°. Зная, что сумма углов треугольника равна 180°, находим угол АВЕ:
<ABE=180-<A-<AEB=180-30-120=30°
Значит треугольник АВЕ - равнобедренный, т.к. углы при его основании АВ равны. Значит АЕ=ВЕ=14.
9. Т.к. АВС - равнобедренный по условию, то углы А и С при его основании АС равны. Прямоугольные треугольники АЕС и CDA равны по одниму из признаков равенства прямоугольных треуг-ов: гипотенуза и острый угол одного прямоугольного треуг-ка соответственно равны гипотенузе и острому углу другого. АС - общая гипотенуза, <A=<C.
2. Поскольку углы А и С равны по условию, треугольник АВС - равнобедренный и АВ=ВС. Из точки В проведен отрезок к основанию АС. Поставим там точку Н, например (я делать этого не буду, обозначь на рисунке точку сам). В треугольниках АВН и НВС по 2 одинаковых угла: <A=<C, <AHB=<СHВ. Исходя из того, что сумма углов треугольника равна 180 градусов, углы АВН и СВН также будут равны. Получаем, что треугольники АНВ и СНВ равны по второму признаку равенства треугольников: сторона и два прилежащих к ней угла одного треугольника соотвественно равна стороне и двум прилежащим к ней углам другого треугольника: АВ=ВС, <A=<C, <ABH=<CBH.
3. Треугольник AED равнобедренный по условию, значит углы EAD и EDA при его основании равны. Получается, что в прямоугольных треугольниках ACD и ABD гипотенуза AD - общая, а острые углы EAD и EDA равны. Следовательно, треугольники ACD и ABD равны по одному из признаков равенства прямоугольных треугольников: гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого.
Прямоугольные треугольники АВЕ и DCE также равны по гипотенузе и катету: АЕ=ED по условию (это гипотенузы), АВ=CD (катеты). Почему эти катеты равны, доказано выше (прямоугольные ACD и ABD равны между собой).
4. Зная, что в прямоугольном треугольнике катет ВС, лежащий против угла в 30 градусов, равен половине гипотенузы АВ, находим АВ:
ВС= АВ : 2, отсюда АВ = ВС * 2 = 4*2=8
5. Зная, что сумма острых углов прямоугольного треугольника равна 90 градусов, находим угол А:
<A=90-<B=90-60=30°
Катет ВС в прямоугольном треугольнике лежит против угла А в 30°, значит, он равен половине гипотенузы АВ:
ВС=АВ:2=10:2=5
6. Зная, что сумма острых углов прямоугольного треуг-ка равна 90°, находим угол А:
<A=90-<B=90-45=45°
Таким образом, треугольник АВС является равнобедренным, поскольку углы при его основании АВ равны. Значит
ВС=АС=6
7. Рассмотрим прямоугольный треуг-ик CDB. Зная, что сумма острых углов прямоугольного треугольника равна 90°, находим угол DCB:
<DCB=90-<B=90-45=45°
Таким образом, получаем, что треуг-ик CDB является равнобедренным, т.к. углы при его основании ВС равны. Значит
CD=BD=8
В прямоугольном треуг-ке АВС угол А равен 90-<B=90-45=45°, он также равнобедренный. Высота CD, проведенная в равнобедренном треугольнике к его основанию, является также и медианой. Значит
BD=AD=8, AB=8+8=16
8. Рассмотрим прямоугольный треугольник ВСЕ. Зная, что сумма острых углов прямоугольного треуг-ка равна 90°, находим угол СВЕ:
<CBE=90-<BEC=90-60=30°
В прямоугольном треугольнике катет, лежащий против угла в 30°, равен половине гипотенузы, значит
ЕС=ВЕ:2, отсюда ВЕ=2*ЕС=2*7=14
В треугольнике АВЕ угол АЕВ равен 180-<BEC=180-60=120°. Зная, что сумма углов треугольника равна 180°, находим угол АВЕ:
<ABE=180-<A-<AEB=180-30-120=30°
Значит треугольник АВЕ - равнобедренный, т.к. углы при его основании АВ равны. Значит АЕ=ВЕ=14.
9. Т.к. АВС - равнобедренный по условию, то углы А и С при его основании АС равны. Прямоугольные треугольники АЕС и CDA равны по одниму из признаков равенства прямоугольных треуг-ов: гипотенуза и острый угол одного прямоугольного треуг-ка соответственно равны гипотенузе и острому углу другого. АС - общая гипотенуза, <A=<C.
Похожие вопросы
Предмет: Биология,
автор: bugagabugaga97
Предмет: Қазақ тiлi,
автор: n100114
Предмет: Английский язык,
автор: Аноним
Предмет: Физика,
автор: myxaxaxa
Предмет: Обществознание,
автор: nikolos11