Question

ПОМОГИТЕ ОЧЕНЬ СРОЧНО ДАЮ МНОГО БАЛЛОВ ПОЖ-ТААААААА
исследуйте функцию и посторойте ее график 
f(x)= -x3+2x2
1)найдите наибольшее и наименьшее значение 
а)f(x)= x4/2-2x3+2x2 на отрезке [-1;2]
б)f(x)=2cos2x-cos4x на отрезке [0;П/2]

Answer 1

a) f'(x)=2x^3-6x^2+4x=2x(x^2-3x+2)=2x(x-1)(x-2)

_-___0__+__1__-___2___+___

минимум f(0)=0; f(2)=8-16+8=0
max f(1)=1/2-2+2=1/2
f(-1)=1/2+2+2=4,5
max = f(-1)=4,5  min f(0)=f(2)=0
б)f'(x)=-4sin2x+4sin4x
sin4x=sin2x
sin2x(2cos2x-1)=0 
x=Пk/2  0; П/2
cos2x=1/2  x=+-П/6+Пk 
               x=П/6
f(0)=2-1=1 ; f(П/2)=2cosП-сos2П=-2-1=-3
f(П/6)=2*1/2-cos(2П/3)=1+1/2=3/2
max=f(п/6)=3/2
min=f(П/2)=-3

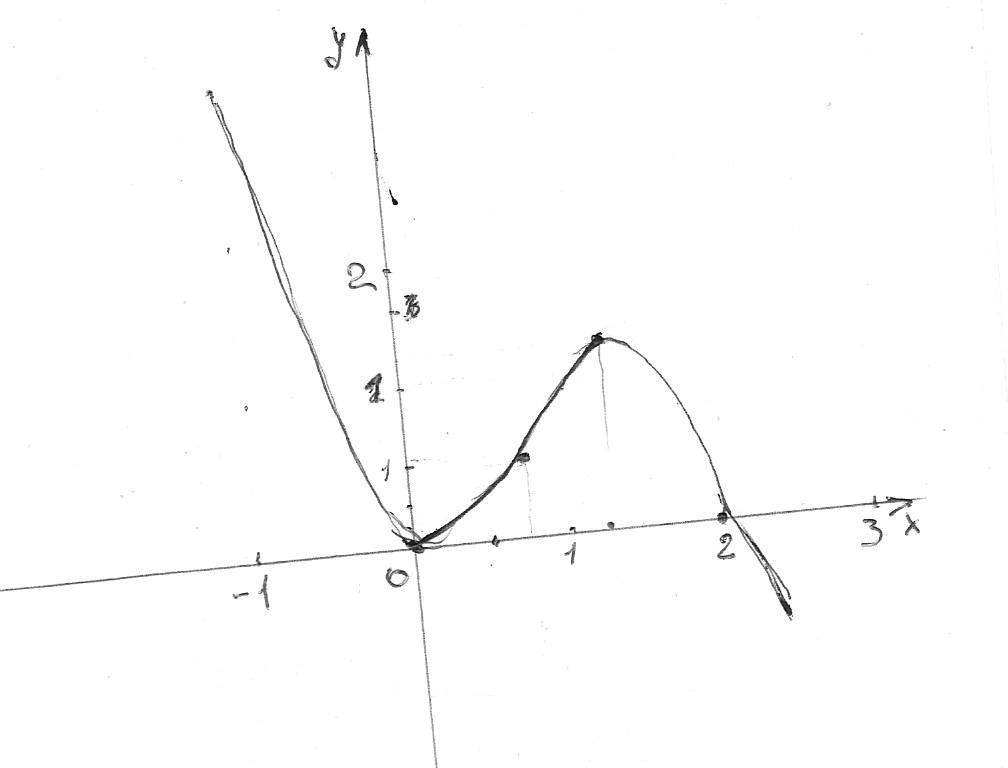
f(x)=-x^3+2x^2
f(0)=0  f(x)=x^2(-x+2)
f(2)=0  нули (0;0) (2;0)
область определений и область значений вся числовая ось.
f'(x)=-3x^2+4x  f'(x)=0  x=0  x=4/3
f(0)- точка минимума
f(4/3) точка максимума.
f''(x)=-6x+4  x=2/3 f(2/3)=16/27  - точка перегиба
асимптот функция не имеет.
f(4/3)=-(4/3)^3+2(4/3)^2=16/9(2-4/3)=32/27
f(-1)=1+2=3