Предмет: Математика,
автор: stnastya137
как решить эти примеры?
(во втором производную надо найти)
Приложения:
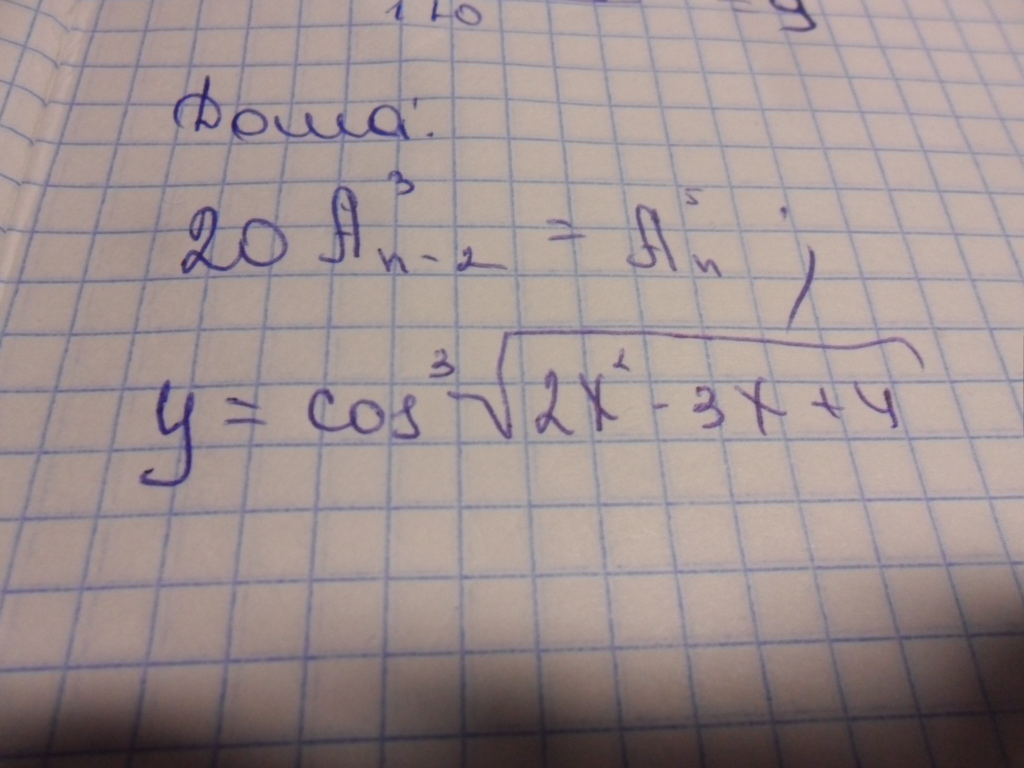
Ответы
Автор ответа:
0
Числитель и знаменатель сокращаем до (n-5), остаётся
Второй корень не подходит, т.к. n - целое положительное число.
Похожие вопросы
Предмет: Русский язык,
автор: rustam6669
Предмет: Математика,
автор: werxlog
Предмет: Английский язык,
автор: omertajdulat
Предмет: История,
автор: ju4kova
Предмет: Литература,
автор: wwwksushechka