Предмет: Геометрия,
автор: Liik
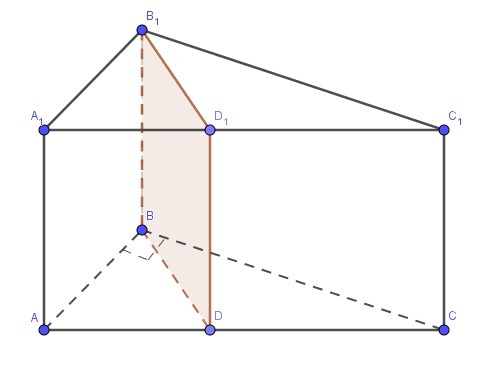
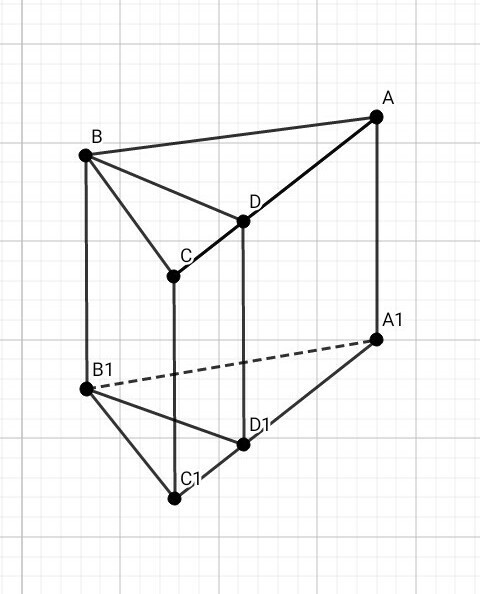
Основанием прямой призмы АВСA1B1C1 является прямоугольный треугольник ABC с прямым углом В. Через ребро ВВ1проведено сечение BB1D1D, перпендикулярное к плоскости грани АA1C1C. Найдите площадь сечения, если AA1 = 10 см, AD = 27 см, DC= 12 см.
Ответы
Автор ответа:
0
Имеем следовательно,
см и поскольку плоскость BB1D1D перпендикулярна к плоскости AA1C1C, то
. Значит, BD - высота прямоугольного треугольника ABC и
- прямоугольник.
Высота, опущенная из вершины прямого угла на гипотенузу, есть среднее пропорциональное между проекциями катетов:
см
Площадь сечения: см².
Ответ: 180 см².
Приложения:
Автор ответа:
0
( ВВ1D1 ) перпендикулярен ( АА1С1 )
Две пересекающиеся плоскости называются перпендикулярными ( взаимно перпендикулярными ), если угол между ними равен 90° →
BD перпендикулярен АС
В1D1 перпендикулярен А1С1
Боковые рёбра прямой призмы равны и перпендикулярны основаниям → АА1 = ВВ1 = СС1 = 10 см
ВВ1 перпендикулярен BD и B1D1
Основания прямой призмы параллельны и равны → BD || B1D1
Соответственно равны и высоты BD и В1D1 прямоугольных треугольников АВС и A1B1C1 ( BD = B1D1 )
Значит, заданное по условию сечение BB1D1D является прямоугольником
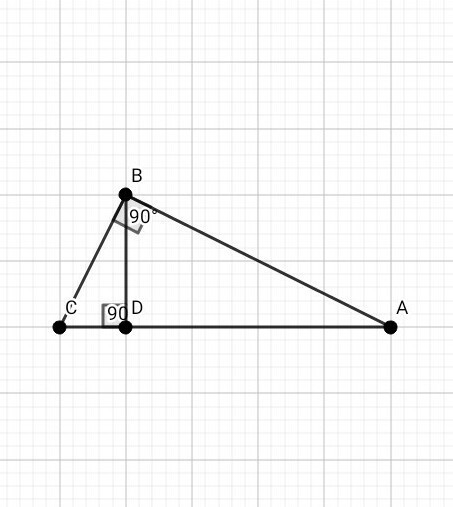
Рассмотрим ∆ АВС (угол В = 90°):
Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу →
BD² = DC × AD
BD² = 12 × 27 = 4 × 3 × 9 × 3
BD = 18 см
Площадь сечения BB1D1D ( прямоугольника ) равна:
S = BB1 × BD = 10 × 18 = 180 см²
ОТВЕТ: S сеч. = 180 см²
Две пересекающиеся плоскости называются перпендикулярными ( взаимно перпендикулярными ), если угол между ними равен 90° →
BD перпендикулярен АС
В1D1 перпендикулярен А1С1
Боковые рёбра прямой призмы равны и перпендикулярны основаниям → АА1 = ВВ1 = СС1 = 10 см
ВВ1 перпендикулярен BD и B1D1
Основания прямой призмы параллельны и равны → BD || B1D1
Соответственно равны и высоты BD и В1D1 прямоугольных треугольников АВС и A1B1C1 ( BD = B1D1 )
Значит, заданное по условию сечение BB1D1D является прямоугольником
Рассмотрим ∆ АВС (угол В = 90°):
Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу →
BD² = DC × AD
BD² = 12 × 27 = 4 × 3 × 9 × 3
BD = 18 см
Площадь сечения BB1D1D ( прямоугольника ) равна:
S = BB1 × BD = 10 × 18 = 180 см²
ОТВЕТ: S сеч. = 180 см²
Приложения:
Похожие вопросы
Предмет: Литература,
автор: levchuk2927
Предмет: Алгебра,
автор: hannakerimova
Предмет: Математика,
автор: Аноним
Предмет: Физика,
автор: msderkaya
Предмет: География,
автор: vjkjrj1972