Укажите количество точек с целочисленными координатами, которые принадлежат области определения функции
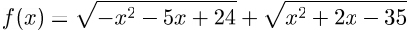
Ответы
Подкоренные выражения не должны быть меньше нуля.
-x²-5x+24>0
x²+5x-24<0
x²+5x-24 = 0
по теореме Виета
x1=-8
x2= 3
(x+8)(x-3)< 0
x<-8, x>3
x>-8, x<3
x ∈ [-8; 3]
x²+2x-35>0
x²+2x-35=0
По теореме Виета
x1= 5
x2=-7
(x-5)(x+7)>0
x>5, x>-7
x<5, x<-7
x ∈ (-∞;-7]U[5; +∞)
Целочисленные абциссы -8 и -7
Проверим ординаты
у(-8)=√(-x²-5x+24)+ √(x²+2x-35)= √-64+40+24 +√64-16+280=√328
y(-7)= √(-x²-5x+24)+ √(x²+2x-35)= √-49+35+24 + 0 = √10
Целочисленных ординат нет ((
Так как сумма 2 иррациональных числа не может быть рациональным если они имеют одинаковые знаки и подкоренные выражения не равны нулю. Так как в данном случае у нас обе корни должны быть положительными то их сумма никогда не будет рациональной, если об подкоренные выражения не будут квадратами чисел.
Теперь найдем область определения каждого выражения:
-x^2-5x+24>0
x^2+5x-24<0
Введем функцию и решим
x1=-8
x2= 3
x принадлежит [-8; 3]
теперь воторое
x^2+2x-35>0
Введем функцию и решим
x1= 5
x2=-7
x принадлежит (-∞;-7]U[5; +∞)
Найдем пересечение [-8; 3] и (-∞;-7]U[5; +∞)
[-7;-8] . Целочисленные x получим -7 -8.
Теперь нужно проверить чтобы при этих значениях y тоже была целочисленной:
Оба они не подходят, значит нет таких точек чтобы и абсцисса и оордината были целочисленными.