Question

нужна помощь срочно пожалуйста объясните решение не могу понять 
Най­ди­те пе­ри­метр че­ты­рех­уголь­ни­ка , если сто­ро­ны квад­рат­ных кле­ток равны квадратный корень из 5

Answer 1

Нужный рисунок к задаче в прикрепленном файле.

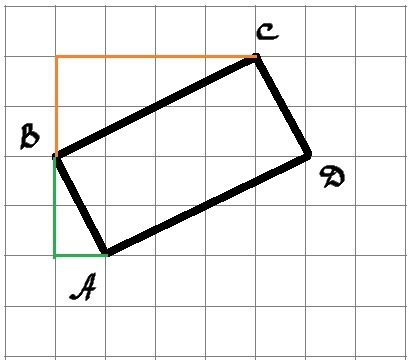
Нужно найти периметр четырехугольника. Значит нам нужно найти длины всех сторон этого четырехугольника, а затем их сложить. По рисунку видно, что противоположные стороны четырехугольника равны.
Поэтому достаточно найти длины смежных сторон АВ и ВС.

Найдем длину стороны АВ.
Достроим её до прямоугольного треугольника (на рисунке выделен зеленым цветом)
Один катет длиной 1 клетка, второй катет - 2 клетки.
Длина стороны клетки $sqrt{5}$.

Значит длина одного катета $sqrt{5}$.
Длина второго катета $2sqrt{5}$

По теореме Пифагора найдем длину гипотенузы этого треугольника.

$AB= sqrt{( sqrt{5})^2+(2 sqrt{5} )^2 } = sqrt{5+20}= sqrt{25} =5$

Найдем длину ВС.

Достроим этот отрезок до прямоугольного треугольника (на рисунке выделен оранжевым цветом).

Длина одного катета 2 клетки, длина второго катета 4 клетки.
Учитывая, что длина стороны клетки $sqrt{5}$, получаем:

один катет длиной $2sqrt{5}$,
второй катет длиной $4sqrt{5}$.

По теореме Пифагора находим длину гипотенузы:

$BC= sqrt{(2 sqrt{5} )^2+(4 sqrt{5} )^2} = sqrt{20+80}= sqrt{100}=10$

$P_{ABCD}=2(AB+BC)=2(5+10)=2*15=30$

Ответ: $P_{ABCD}=30$