Предмет: Геометрия,
автор: Марина1912
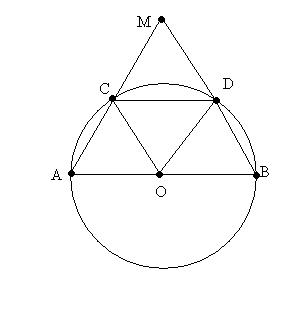
Дана окружность с цетром О и диаметром АВ. Вне окружности зята точка М, так что прямые МА и МВ пересекают окружность в точках С и D соответственно; АС=СD=BD. Докажите, что АС=ОВ
Ответы
Автор ответа:
0
АС=СD=DB половина окружности разбита на 3 равные части, следовательно угол АСD равен 180:3=60°, а отрезки AO и СО - радиусы, мы получили равносторонний тр-к, аналогично остальные треугольники. Следовательно АС равна радиусу ОВ.
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: fgsrighsy
Предмет: Русский язык,
автор: polina9315
Предмет: Математика,
автор: batyrgalievamira1986
Предмет: Математика,
автор: zarina2000