Предмет: Геометрия,
автор: Anastasia11111997
Терміново потрібна допомога!!! Із деякої точки до площини проведено дві похилі, кожна з яких завдовжки 4см.Знайдіть відстань між основами цих похилих,якщо кут між проекціями дорівнює 120 градусів, а кут який кожна похила утворює з площиною, становить 30 градусів.
Ответы
Автор ответа:
0
Не гарантую, що саме так, але на результат вийшов))
Sqrt(x) – корінь, де х любе число
^х – квадрат, де х любе число
Проводимо перепендикулярну пряму до площини ОВ. Похилі ОА і ОС під кутом 30 градусів до площини, їх проекції АВ і ВС утворють кут 120 градусів Оскільки ОB перпендикулярна до площини, то трикутники АВО і СВО є прямокутними трикутниками АО=ОС=4 см по умовах завдання
Трегометричне співвідношення для прямокутних трикутників:
cos30º=AВ/AО
AВ=AО cos30º=4 cos30º=2sqrt(3)
За теоремою косинусів: АС² = АВ² + ВС² - 2 * АВ * ВС * cos120
АС² = (2sqrt3)^2+ (2sqrt3)^2 – 2 * 2sqrt(3) * 2sqrt(3) * cos120 cos120 = - 0,5
АС² = 12 + 12 – * 2 * 2sqrt(3) * 2sqrt(3) * (-0,5)
АС² = 24 – (-12) АС² = 36 АС = sqrt(36)
АС = 6
Відповідь – відстань між основами цих похилих 6 см
Sqrt(x) – корінь, де х любе число
^х – квадрат, де х любе число
Проводимо перепендикулярну пряму до площини ОВ. Похилі ОА і ОС під кутом 30 градусів до площини, їх проекції АВ і ВС утворють кут 120 градусів Оскільки ОB перпендикулярна до площини, то трикутники АВО і СВО є прямокутними трикутниками АО=ОС=4 см по умовах завдання
Трегометричне співвідношення для прямокутних трикутників:
cos30º=AВ/AО
AВ=AО cos30º=4 cos30º=2sqrt(3)
За теоремою косинусів: АС² = АВ² + ВС² - 2 * АВ * ВС * cos120
АС² = (2sqrt3)^2+ (2sqrt3)^2 – 2 * 2sqrt(3) * 2sqrt(3) * cos120 cos120 = - 0,5
АС² = 12 + 12 – * 2 * 2sqrt(3) * 2sqrt(3) * (-0,5)
АС² = 24 – (-12) АС² = 36 АС = sqrt(36)
АС = 6
Відповідь – відстань між основами цих похилих 6 см
Приложения:
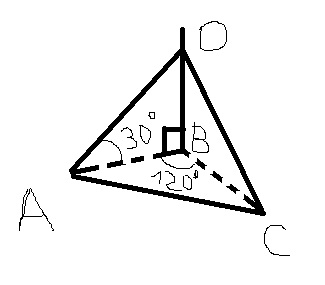
Похожие вопросы
Предмет: Русский язык,
автор: kacajanna010
Предмет: Английский язык,
автор: dmitrijkosatyj
Предмет: Математика,
автор: Аноним
Предмет: Обществознание,
автор: alinapylaeva
Предмет: Химия,
автор: Lacarna96