найдите область определения функции
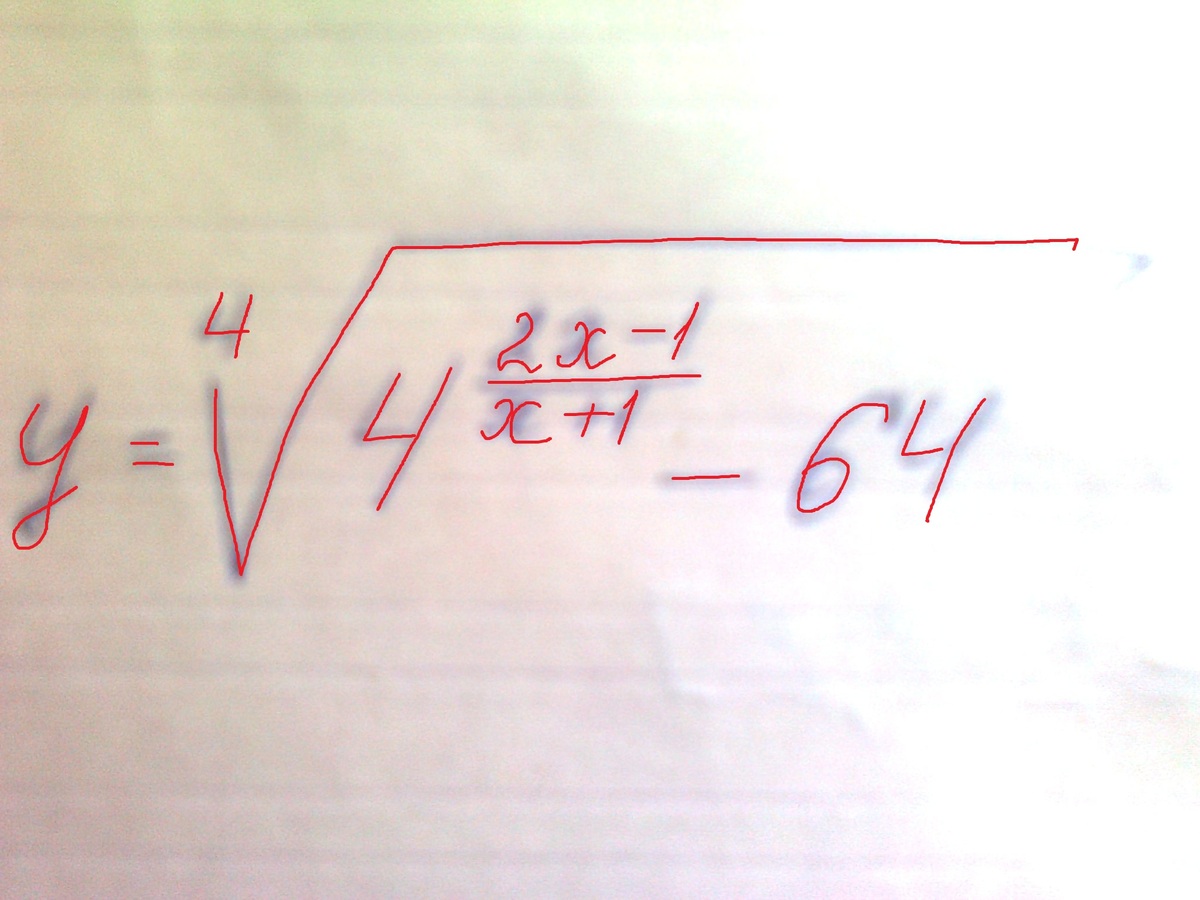
Ответы
Использовано сравнение степеней при основании >1, метод интервалов

у = (4^((2х - 1)/(x + 1)) - 64)^0.25
Разложим подкоренное выражение на множители
у = [(2^((2х - 1)/(x + 1)) - 8)·(2^((2х - 1)/(x + 1)) + 8)]^0.25
Подкоренное выражение не должно быть отрицательным.
Рассмотрим второй множитель подкоренного выражения:
2^((2х - 1)/(x + 1)) + 8
в нём
8 > 0
и
2 в любой степени больше нуля, поэтому весь множитель
2^((2х - 1)/(x + 1)) + 8 > 0.
Тогда и 1-й множитель должен быть неотрицательным, т.е.
(2^((2х - 1)/(x + 1)) - 8) ≥ 0
2^((2х - 1)/(x + 1)) - 2^3) ≥ 0
2^((2х - 1)/(x + 1)) ≥ 2^3
Поскольку основание степени 2 > 1, то отношение между степенями такое же, как и между числами, т.е.
(2х - 1)/(x + 1) ≥ 3
Знаменатель дроби не должен быть равен нулю, поэтому
х ≠ -1
1) Если х + 1 > 0 , то х > -1
2х - 1 ≥ 3·(х + 1)
2х - 1 ≥ 3х + 3
х ≤ -4 не согласуется с х > -1
Таким образом, неравенство х + 1 > 0 неверное, т.е остаётся предположить, что
х + 1 < 0
2) Если х + 1 < 0, то х < -1
2х - 1 ≤ 3·(х + 1)
2х - 1 ≤ 3х + 3
х ≥ -4 согласуется с х < -1
Таким образом, область определения D(y) = [-4; -1)
