Предмет: Геометрия,
автор: PruFFI
Хорда окружности равна а и стягивает дугу в 120°. Найдите:
а) длину дуги
б) площадь сектора ограниченного этой дугой и двумя радиусами
Ответы
Автор ответа:
0
Дуга равна центральному углу, который на нее опирается
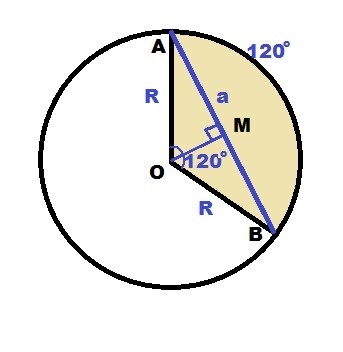
∠AOB = ∪AB = 120°
ΔAOB - образован хордой и двумя радиусами ⇒ равнобедренный
OM - высота, она же биссектриса и медиана ⇒ AM = a/2
∠AOM = ∠BOM = 120°/2 = 60°
ΔAOM - прямоугольный

Длина дуги

Площадь сектора

∠AOB = ∪AB = 120°
ΔAOB - образован хордой и двумя радиусами ⇒ равнобедренный
OM - высота, она же биссектриса и медиана ⇒ AM = a/2
∠AOM = ∠BOM = 120°/2 = 60°
ΔAOM - прямоугольный
Длина дуги
Площадь сектора
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: huhuhu14
Предмет: География,
автор: svetlanagoranova6
Предмет: История,
автор: vvhvh567
Предмет: Математика,
автор: nastya1215