Question

основание пирамиды правильный треугольник с площадью 36корней из 3. Две боковые грани перпендикулярны к плоскости основания, а третья наклонена к ней под углом 30 градусов. найти площадь боковой поверхности пирамиды

Answer 1

Использованы: формула площади правильного треугольника, формула высоты правильного треугольника, определение тангенса, косинуса, формула площади треугольника

Answer 2

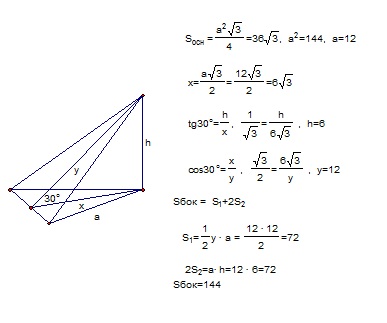
Боковая поверхность пирамиды равна сумме площадей 3х граней (треугольников)

Высота основания h=a√3/2,  площадь основания S = a*h/2 = a²√3/4, отсюда

а = √4S/√3 = √4*36√3/√3 = 12

Высота пирамиды H = h*tg 30 = 6√3*1/√3 = 6, апофема А=√h²+Н²=√36*3+36=12

S = a*H/2+a*H/2+a*A/2 = 12*6+12*12/2 = 72+72 = 144