Question

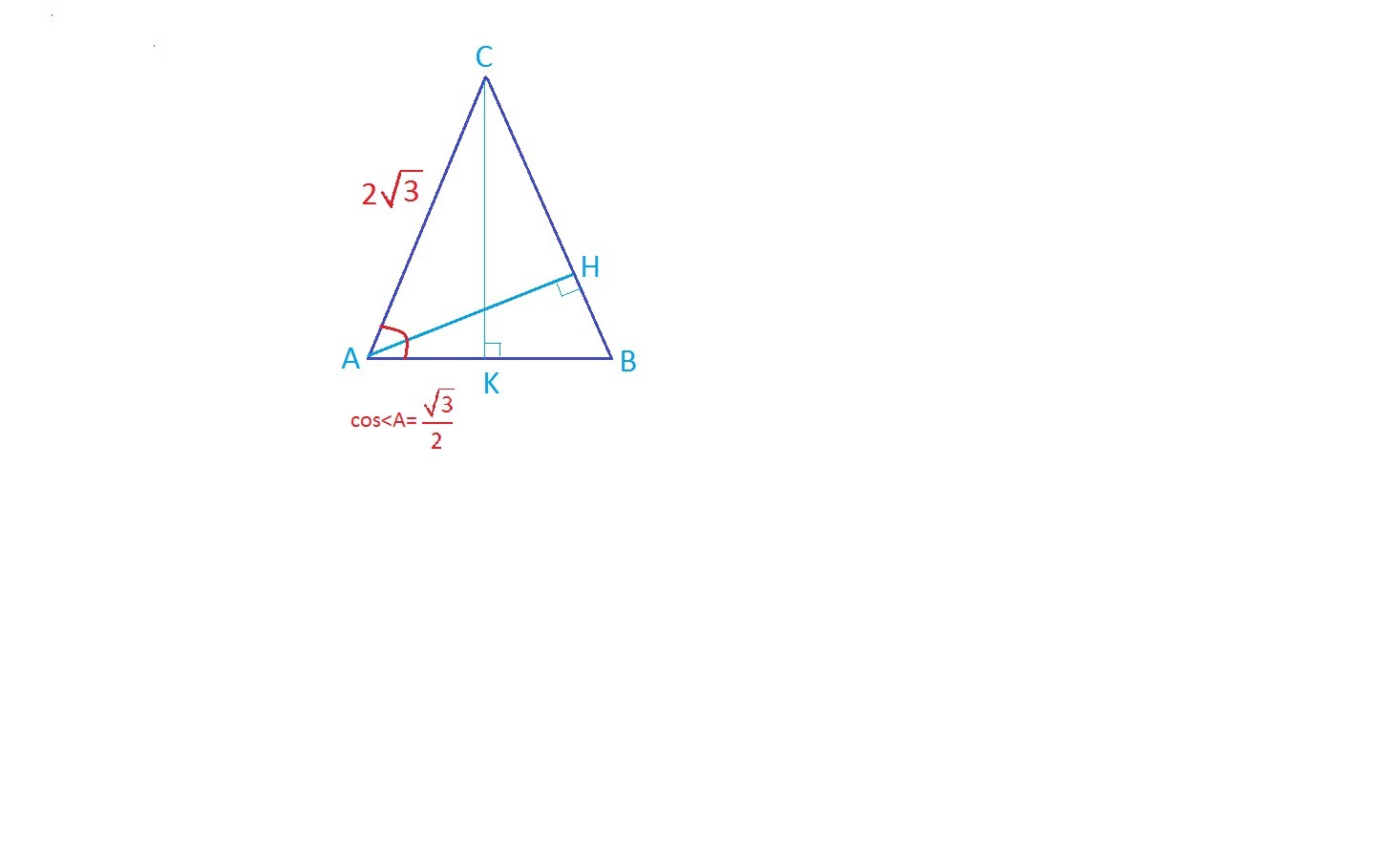
в равнобедренном треугольнике ABC с основанием AB боковая сторона AC равна 2√3 а cos угла A корень из 3/2.Найдите длину высоты AH этого треугольника.

Answer 1

Δ $ABC-$ равнобедренный
$AB-$ основание
$AC=2 sqrt{3}$
$cos textless A= frac{ sqrt{3} }{2}$
$AH-$ ?

Δ $ABC-$ равнобедренный
$AC=CB$
$textless A= textless B$ ( по свойству углов при основании  равнобедренного треугольника)
$cos textless A= frac{ sqrt{3} }{2}$  ⇒ $textless A=30к$
$textless A= textless C=30к$
$CK$ ⊥ $AB$
Δ $CKA-$ прямоугольный
$frac{AK}{AC} =cos textless A$
$AK=AC*cos textless A$
$AK=2 sqrt{3} * frac{ sqrt{3} }{2} =3$
$AK=KB$
$AB=2AK=2*3=6$
$AH$ ⊥ $BC$ (по условию)
Δ $AHB-$ прямоугольный
$frac{AH}{AB}=sin textless C$
$AH=AB*sin textless C$
$AH=6*sin30к=6* frac{1}{2} =3$

Ответ: 3

Answer 2

Если вспомнить, что $frac{ sqrt{3} }{2}$ - это косинус 30°,
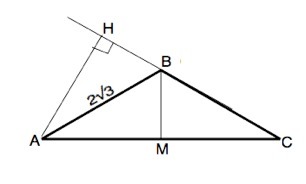
то , т.к. ∆ АВС равнобедренный, ∠АСВ=∠САВ=30°, и ∠АВС=120°. Треугольник АВС - тупоугольный, высота АН проводится к продолжению ВС, и ∠АВН=60° как смежный углу АВС. Тогда АН=АВ•sin60°=$2 sqrt{3}$•$frac{ sqrt{3} }{2}$=3 (ед. длины)
Как вариант можно найти сторону АС.  Если ВМ - высота ( медиана, биссектриса) равнобедренного ∆ АВС, то АМ=АВ•cos∠A= AB•$frac{ sqrt{3} }{2}$ =3 ⇒АС=2•AH=6

В равнобедренном ∆ АBС ∠С=∠А. ⇒ синус ∠С=√(1-cos²A)=√(1-3/4)=1/2
АН=АС•sin 30°=6:2=3 (ед. длины)