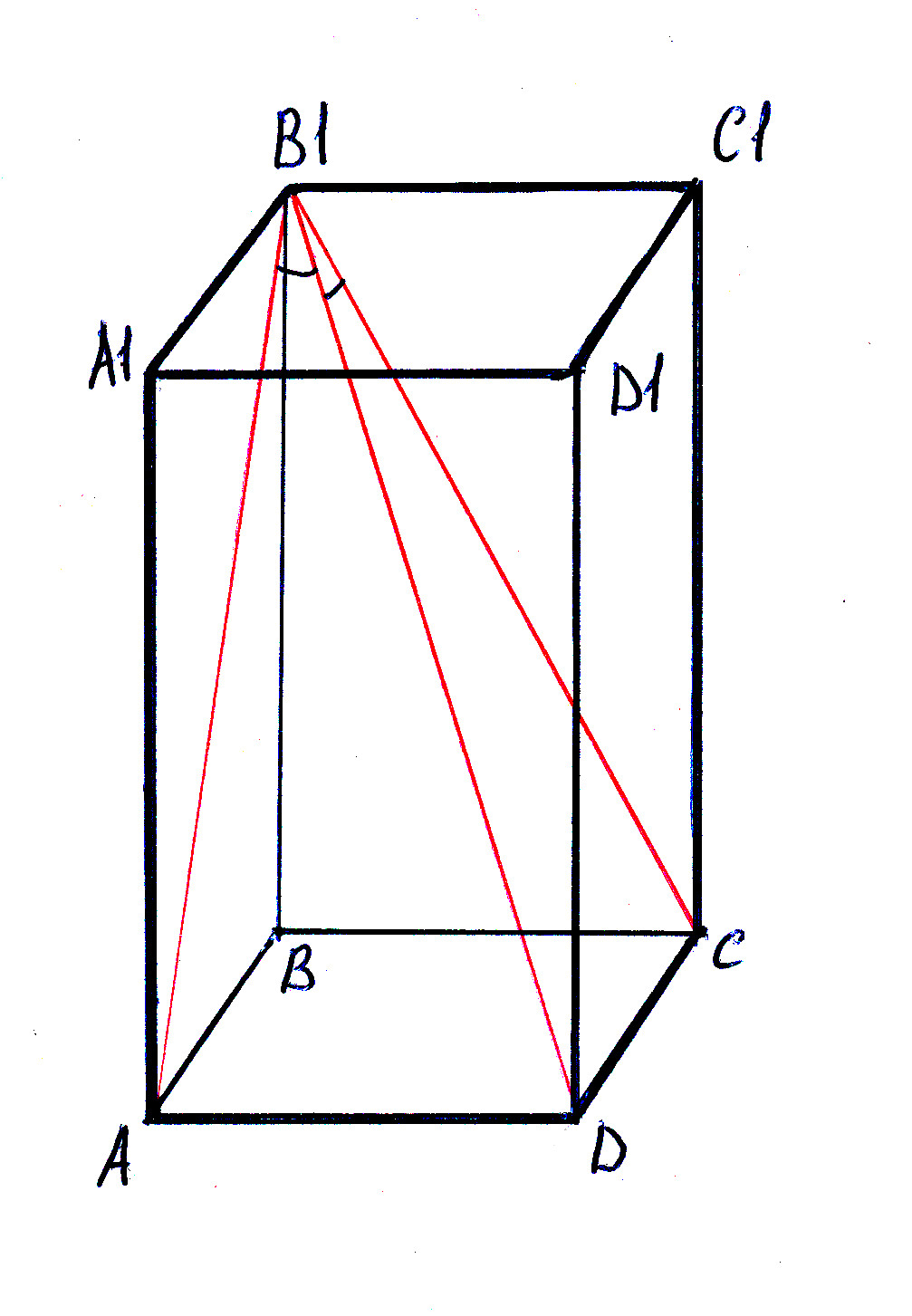
Диагональ прямоугольного параллелепипеда образует с двумя его гранями, имеющими общее ребро, равные углы. докажите,что грань,перпендикулярная к этому ребру- квадрат.
Ответы
диагональ параллелепипеда=А
общее ребро=B
грань, перпендикулярная В=Z.
диагональ грани, перпендикулярной В=X. поехали
А-наклонная к плоскости Z, a X проекция наклонной A на плоскости Z. По теореме о трех перпендикулярах: если диагональ прямоугольного параллелепипеда образует с двумя его гранями, имеющими общее ребро, равные углы, то и проекция этой диагонали на плоскость Z действует аналогично, более того, проекция наклонной А бедет диагональю прямоугольника, лежащего в основании параллелепипеда. А условие бедет выполняться только тогда, когда прямоугольник, лежащий в основании параллелепипеда, вляется квадратом!
На чертеже видно,что в случае равенства отмеченных углов (угол АВ1D = угол СВ1D) прямоугольные треугольники АВ1D и СВ1D равны. Поэтому равны стороны AD = DC, чтд.