Предмет: Геометрия,
автор: lu4nico
В остроугольном треугольнике ABC проведена высота BN. Синус угла BAC равен 0,6.
Длина стороны AB равна 20 см, длина стороны BC равна 15 см.
Найдите NC.
Если можно, то с объяснениями, пожалуйста. Хотелось бы понять.
Ответы
Автор ответа:
0
Синус - это отношение катета, противолежащего острому углу прямоугольного треугольника, к гипотенузе.
ВN- высота и перпендикулярна АС.
⊿ АВN - прямоугольный.
sin ВАС=BN:AB
BN:20=0,6
BN=20*0,6=12 см
В прямоугольном треугольнике ВNC нам известны гипотенуза и катет.
По т.Пифагора квадрат гипотенузы равен сумме квадратов катетов:
ВС ²=ВN ²+NC ² ⇒
NC ² = ВС ²-ВN ²
NC²=225-144=81
NC=√81=9 см
ВN- высота и перпендикулярна АС.
⊿ АВN - прямоугольный.
sin ВАС=BN:AB
BN:20=0,6
BN=20*0,6=12 см
В прямоугольном треугольнике ВNC нам известны гипотенуза и катет.
По т.Пифагора квадрат гипотенузы равен сумме квадратов катетов:
ВС ²=ВN ²+NC ² ⇒
NC ² = ВС ²-ВN ²
NC²=225-144=81
NC=√81=9 см
Приложения:
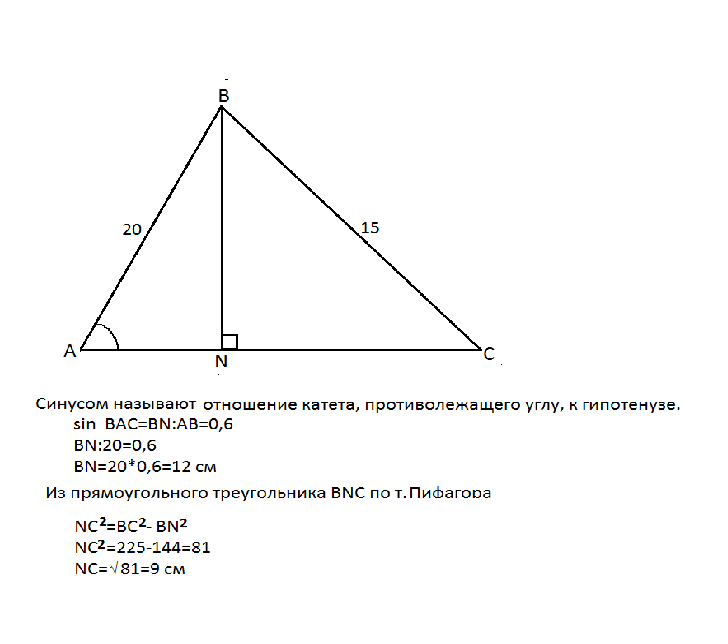
Похожие вопросы
Предмет: Физика,
автор: sadovnichiy0108
Предмет: Обществознание,
автор: Аноним
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Алгебра,
автор: Pichenya
Предмет: Физика,
автор: 901234567