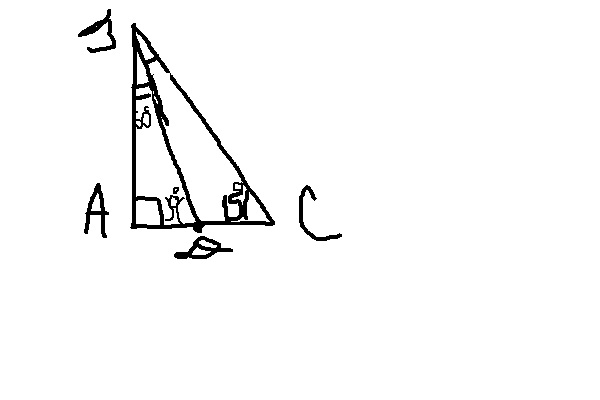В прямоугольном треугольнике ABC катет AB равен 3см угол C равен 15 градусов.На катете AC отмечена точка D так что угол CBD равен 15 градусов.Найдите длину отрезка BD.И напишите что писать в дано и найти и прочее.
Ответы
Дано: треуг. ABC (угол A=90)
угол DCB=углу DBC=15
AB=3cм
Найти: DB
Решение:
Т к угол DCB=углу DBC=15, то найдем угол CDB=180-(15+15)=50, значит можно найти угол ADB=180-50=30
Т к дан прямоугольный треугольник, то катет (AB) лежащий против угла в 30 равен половине гипотенузы, а значит гипотенуза (DB) ,будет равна двум катетам. DB=2*3=6cм
ОТВЕТ: 6см
Дано:
ΔABC,<A=90°
AB=3 см
<C = 15°
<CBD = 15°
Найти:
BD
Решение:
1)Сумма острых углов прямоугольного треугольника равна 90°. Значит, <B = 90° - 15° = 75°
2)Так как <CBD = 15°, а <ABD = <B - <CBD, то <ABD = 75° - 15° = 60°
3)Рассмотрим ΔABD, <A = 90°. Сумма его острых углов опять же равна 90°. значит, <ADB = 90° - 60° = 30°. AB - катет, лежащий против угла в 30°, BD - гипотенуза. А катет, лежащий против угла в 30°, равен половине его гипотенузы. Значит, BD = 2AB = 3 * 2 = 6 см