Предмет: Геометрия,
автор: Learа
Найдите площадь трапеции, диагонали которой равны 17 и 9, а средняя линия равна 5.
Ответы
Автор ответа:
0
Выведу обобщённую формулу для подобных задач про трапецию с известными диагоналями AC = x, BD = y, и суммой оснований BC + AD = m
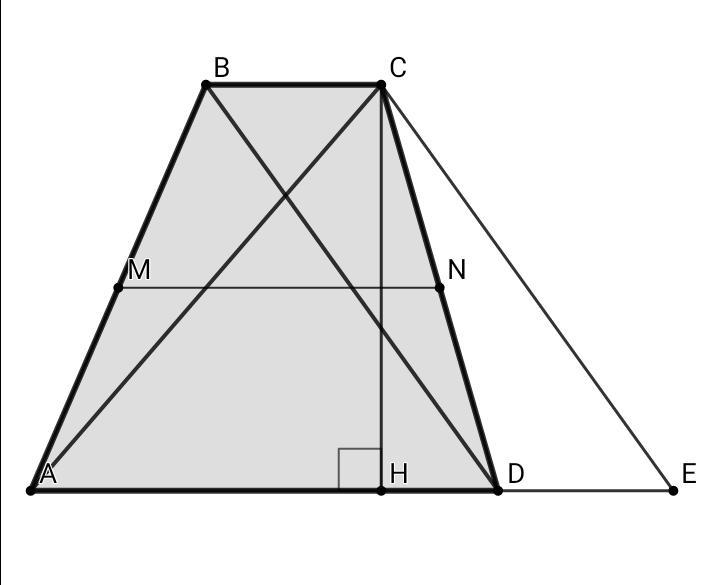
Проведём из вершинны С прямую СЕ, параллельную BD, тогда BC || DE, CE || BD ⇒ BCED - параллелограми, ВС = DE, CE = BD = y
S (abcd) = (BC + AD)•CH/2 = (DE + AD)•CH/2 = AE•CH/2 = S (ace)
Площадь трапеции ABCD равна площади треугольника ACE
Найдём плошадь ΔАСЕ по формуле Герона: АС = х, CE = y, AE = m
Площадь трапеции с диагоналями х и у и суммой оснований равной m:
S = √( p • (p - x) • (p - y) • (p - m) ) , где р = (х + y + m)/2
Средняя линия трапеции: MN = (BC + AD)/2 = 5 ⇒ m = 10, x = 9, у = 17
S (abcd) = √(18•(18 - 9)(18 - 17)(18 - 10)) = √(18•9•1•8) = 36
Ответ: 36
Приложения:
Похожие вопросы
Предмет: Литература,
автор: Аноним
Предмет: Алгебра,
автор: Аноним
Предмет: Химия,
автор: 0millerkahiller
Предмет: Химия,
автор: zarino4ka111
Предмет: Математика,
автор: 20Nina01