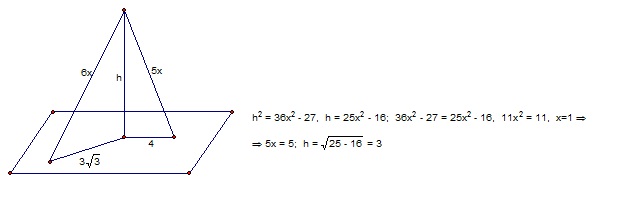из точки к плоскости проведены две наклонные,длины которых относятся,как 5:6.Найдите расстояние от точки до плоскости,если длины соответствующих проекций наклонных на плоскость равны 4 см и 3корня3 см
Ответы
использована теорема Пифагора, определение расстояния между точкой и плоскостью
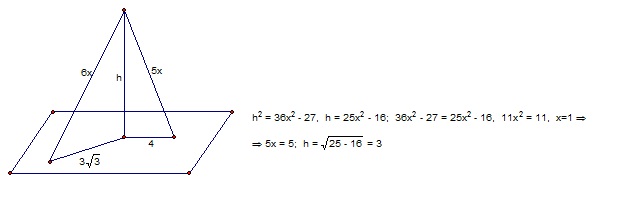
Пусть даны наклонные АВ и АС и перпендикуляр к плоскости АО. Если х - коэффициент пропорциональности, то АВ=5х, АС=6х. Проецией наклонной АВ является отрезок ВО=4 см, а проекцией наклонной АС является отрезок СО=3корня из3. Найдем АО из треугольника АВО по теореме Пифагора: АО^2=AB^2-BO^2=25x^2-16; найдем АО из треугольника АСО по теореме ПИфагора: АО^2=АС^2-CO^2=36x^2-27.Приравняем правые части получившихся выражений 25х^2-16=36x^2-27
11x^2=11
x=1 - коэффициент пропорциональности, то АВ=5 см и АО=3 см
Ответ: 3 см