Question

Что нибудь помогите, хотя бы один очень прошу. Осталось сдать последнюю работу, конец учебного года. Голова взрывается.

Answer 1

4) α - угол наклона касательной;
tgα = f ' (x0) (значение производной в точке касания)
f ' = √3/(x^2)
f'(x0) = √3/1 = √3 = tgα
α = π/3 = 60 градусов

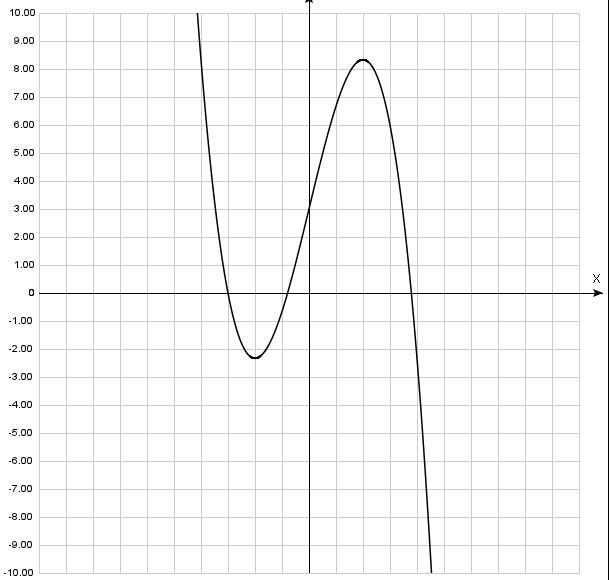
5) Для определения точек экстремума необходимо найти производную.
f ' = -3(x^2)/3 + 4 = -(x^2) + 4 = 0
f ' > 0 при x∈(-бесконечность; -2)U(2; +бесконечность), функция возрастает
f ' < 0 при x∈(-2;2), функция убывает.
x = -2 - точка перегиба, функция выпукла вверх.
x = 2 - точка перегиба, функция выпукла вниз.
Нули функции: f(x) = 0, (-1/3)*x^3 + 4x + 3 = 0
(-1/3)*x^3 + 4x + 3 = (x + 3)((-1/3)x^2 + x + 1) = 0
x1 = -3, x2 = (3-√21)/2, x3 = (3+√21)/2 - нули функции.
Пересечение с осью Оу: x=0, f(0) = 3. график в прикреплении.

Answer 2

спасибо огромнейшее!!!