Question

Помогите пожалуйста!!
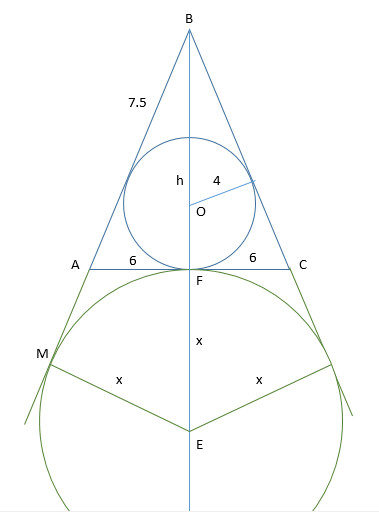
Основание АС равнобедренного треугольника АВС равно 12, а радиус вписанной в него окружности равен 4. Найдите радиус окружности, которая касается продолжения боковых сторон треугольника и касается основания АС в его середин.

Answer 1

Пусть АВ=а, BF=h
h²=a²-6²
Площадь треугольника АВС
S=АС*h=12h=12√(a²-6²)
Полупериметр
p=(2a+12)/2=a+6
Радиус вписанной окружности 
r=S/p
4=12√(a²-6²)/(a+6)
1=3√(a-6)√(a+6)/(a+6)
1=3√(a-6)/√(a+6)
1=9(a-6)/(a+6)
a+6=9a-54
8a=60
a=15/2=7.5
h=√7.5²-36=√20,25=4.5
Треугольники BEM и BAF прямоугольные с равным углом при вершине В. Следовательно, они подобные
AF:AB=ME:BE
6/7.5=x/(4.5+x)
6(4.5+x)=7.5x
26+6x=7.5x
1.5x=26
x=26/1.5=52/3=17 целых 1/3
Ответ: 
$17 frac{1}{3}$