В треугольнике АВС из вершины С проведены два луча, делящие угол АСВ на три равные части. Найти отношение длин отрезков этих лучей, заключённых внутри треугольника, если |ВС| : |АС| = 3, ĿАСВ = а.
Ответы
ну, вроде разобрался.В левой части второго вложенного файла выводится формула длины биссектрисы
l = 2*a*b*cos(C/2)/(a + b);
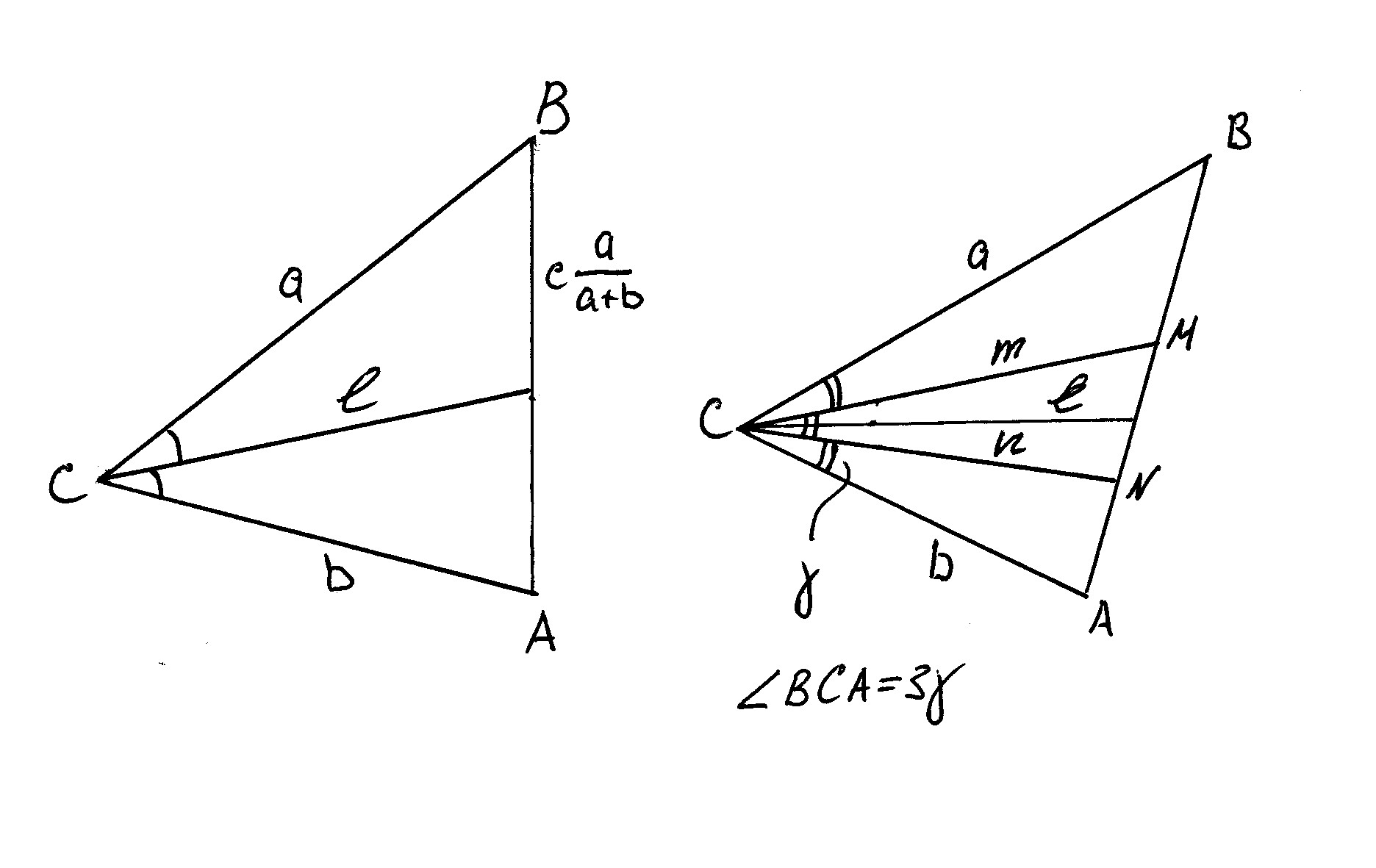
чертеж для этого вывода - это левый треугольник на первом рисунке (вложении).
Второй треугольник на первом рисунке относится к задаче. Все обозначения - на этом чертеже. Требуется найти x = m/n; вывод - на втором вложении. Всё ,что нужно сообразить - это что биссектриса АВС - одновременно биссектриса MNC.
Окончательный ответ
x = (1 + K/b)/(1 + K/a); где К = u*a*b/(a+b); u = cos(C/2)/cos(C/6);
Для случая, когда b = 3*a, как задано в условии,
K/a = u*b/(a + b) = u*3/(1 + 3) = 3*u/4;
K/b = u*a/(a + b) = u/4;
x = (1 + u/4)/(1 + 3*u/4); где u = cos(C/2)/cos(C/6); это и есть ответ. И ничего тут нельзя больше сделать.
Если С = 90 градусов (АВС - прямоугольный треугольник), то
u = cos(45)/cos(15);
cos(45) = корень(2)/2;
cos(15) = (корень(3) + 1)/(2*корень(2));
u = корень(3) - 1;