Предмет: Геометрия,
автор: Kiruru
1. В треугольнике ABC угол C равен 90(градусов), AC = 18, tgA = 4√65/65. Найдите высоту CH.
Ответы
Автор ответа:
0
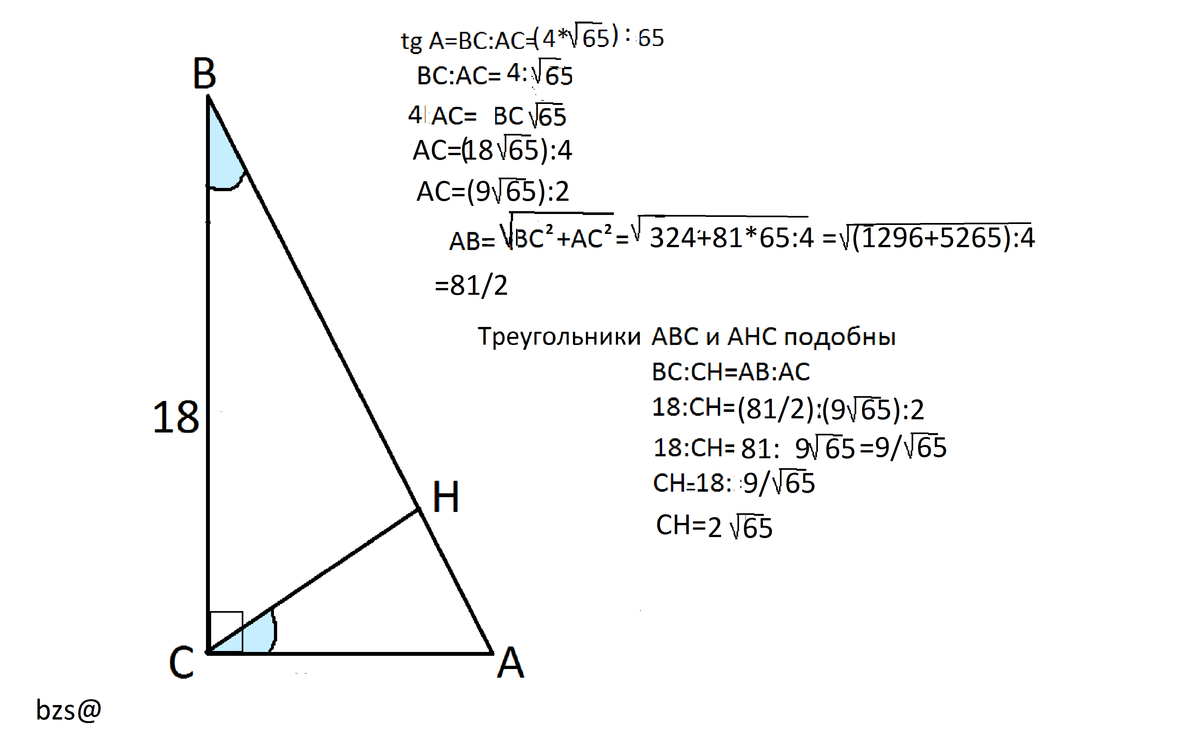
. В треугольнике ABC угол C равен 90 градусов, BC=18, tgA= (4√65)/65.
Найдите высоту CH.
Тангенс находят делением катета, противолежащего углу, к катету прилежащему
Сложность здесь в основном в вычислениях - числа довольно неудобные.
tgA=BC:AC
tgA=(4√65):65
умножим обе части отношения на √65 и получим
(4*√65):65=4:√65
BC:AC=4:√65
4AC=BC*√65
АС=(18√65):4= (9√65):2
Треугольники АВС и АНС подобны по свойству высоты прямоугольного треугольника.
Найдем гипотенузу АВ:
АВ=√(ВС²+АС²)=√(324+81*65:4)=√(6561/4)
АВ=81/2
ВС:СН=АВ:АС
18:СН=(81/2):{(9√65):2}
18 CH=9:√65
CH=18:(9:√65)=2√65
--------
[email protected]
Найдите высоту CH.
Тангенс находят делением катета, противолежащего углу, к катету прилежащему
Сложность здесь в основном в вычислениях - числа довольно неудобные.
tgA=BC:AC
tgA=(4√65):65
умножим обе части отношения на √65 и получим
(4*√65):65=4:√65
BC:AC=4:√65
4AC=BC*√65
АС=(18√65):4= (9√65):2
Треугольники АВС и АНС подобны по свойству высоты прямоугольного треугольника.
Найдем гипотенузу АВ:
АВ=√(ВС²+АС²)=√(324+81*65:4)=√(6561/4)
АВ=81/2
ВС:СН=АВ:АС
18:СН=(81/2):{(9√65):2}
18 CH=9:√65
CH=18:(9:√65)=2√65
--------
[email protected]
Приложения:
Автор ответа:
0
перепутала значение тангенса. Изменю решение
Похожие вопросы
Предмет: Биология,
автор: frodik95
Предмет: Математика,
автор: loginez111
Предмет: Английский язык,
автор: gulnaz073
Предмет: История,
автор: evqenia9
Предмет: Геометрия,
автор: Karinka32