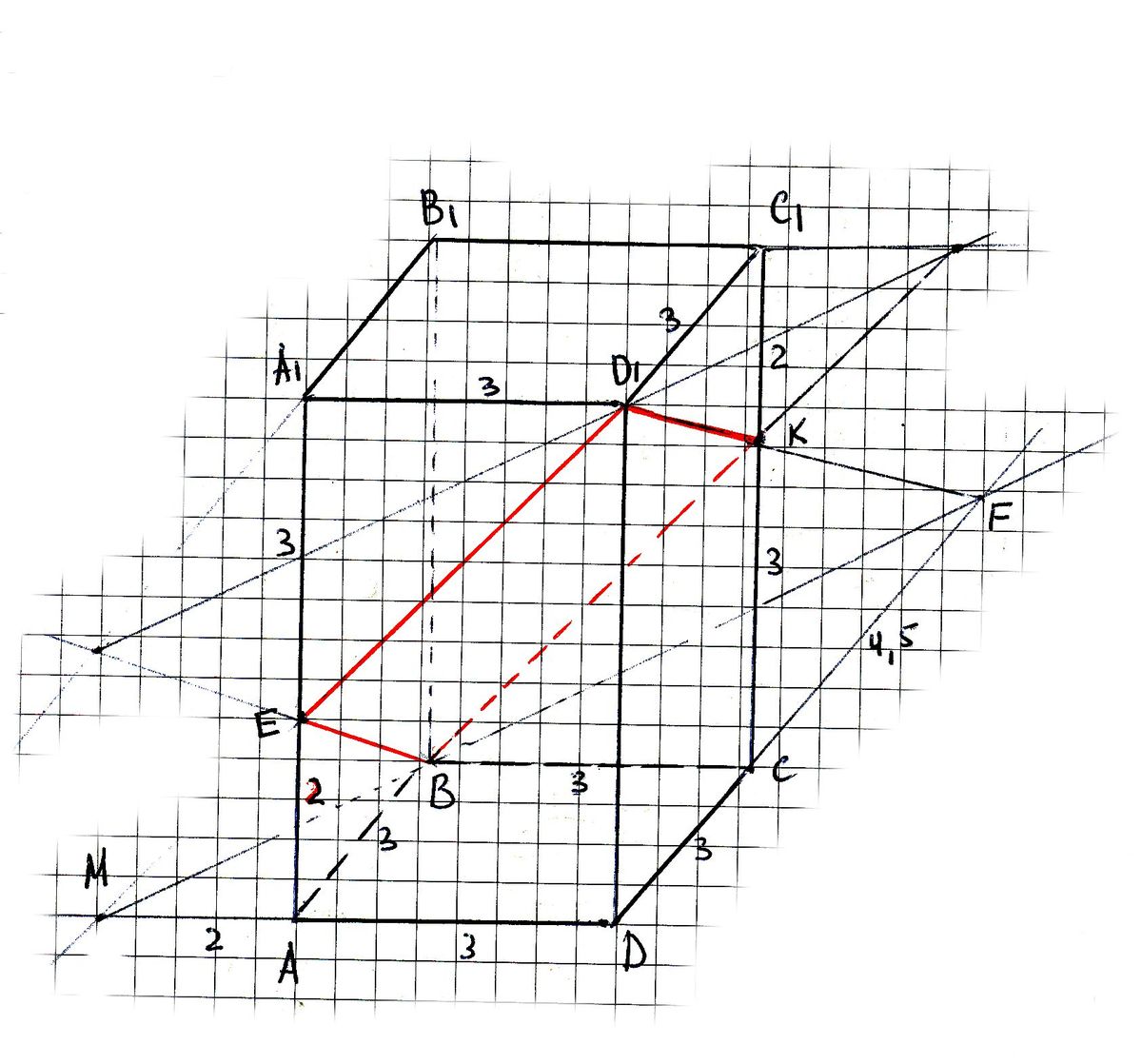
В правильной четырехугольной призме стороны основания равны 3, боковые ребра равны 5. На ребре АА1 отмечена точка Е так што АЕ:ЕА1 =2:3. Найдите угол между плоскостью АВС и ВЕД1.
Ответы
Ясно, что АЕ = 2, ЕА1 = 3. Линия пересечения АВС и ВЕD1 строится так. Продлевается АD за точку А до пересечения М с продолжением D1E. Через точку М и точку В в плоскости АВСD проводится прямая до пересечения с продолжением DC, это точка F. F и D1 соединяются в плоскости DCC1D1. Точка пересечения D1F c С1С - точка К соединяется с В. Четырехугольник ВЕD1K - сечение, прямая МF - линия пересечения АВС и ВЕD1.
Тр-ки А1ЕD1 и МЕА подобны, откуда МА = 2. Треугольники ВСF и МАВ подобны, поэтому FC = 9/2 (я проставил все размеры на чертеже, в том числе и вычисляемые). Получился треугольник DMF со сторонами MD = 5, DF = 15/2 = 7,5;
Очевидно, что если из вершины прямого угла этого треугольника провести перпендикуляр на MF и соединить его основание с D1, то получится искомый линейный угол двугранного угла (обозначим Ф). Поэтому нам надо определить в треугольнике DMF высоту к гипотенузе MF (обозначим h), тогда тангенс угла Ф будет равен DD1 = 5, деленному на эту высоту.
MFD - прямоугольный треугольник с катетами 5 и 7,5,
гипотенуза равна с = 5*корень(13);
высота h = 5*7,5/с;
tg(Ф) = 5/h = c/7,5 = 2*корень(13)/3;