Дан полукруг с диаметром АВ. Через середину полуокружности проведены две прямые, делящие полукруг на три равновеликие части. В каком отношении они делят диаметр АВ?
Ответы
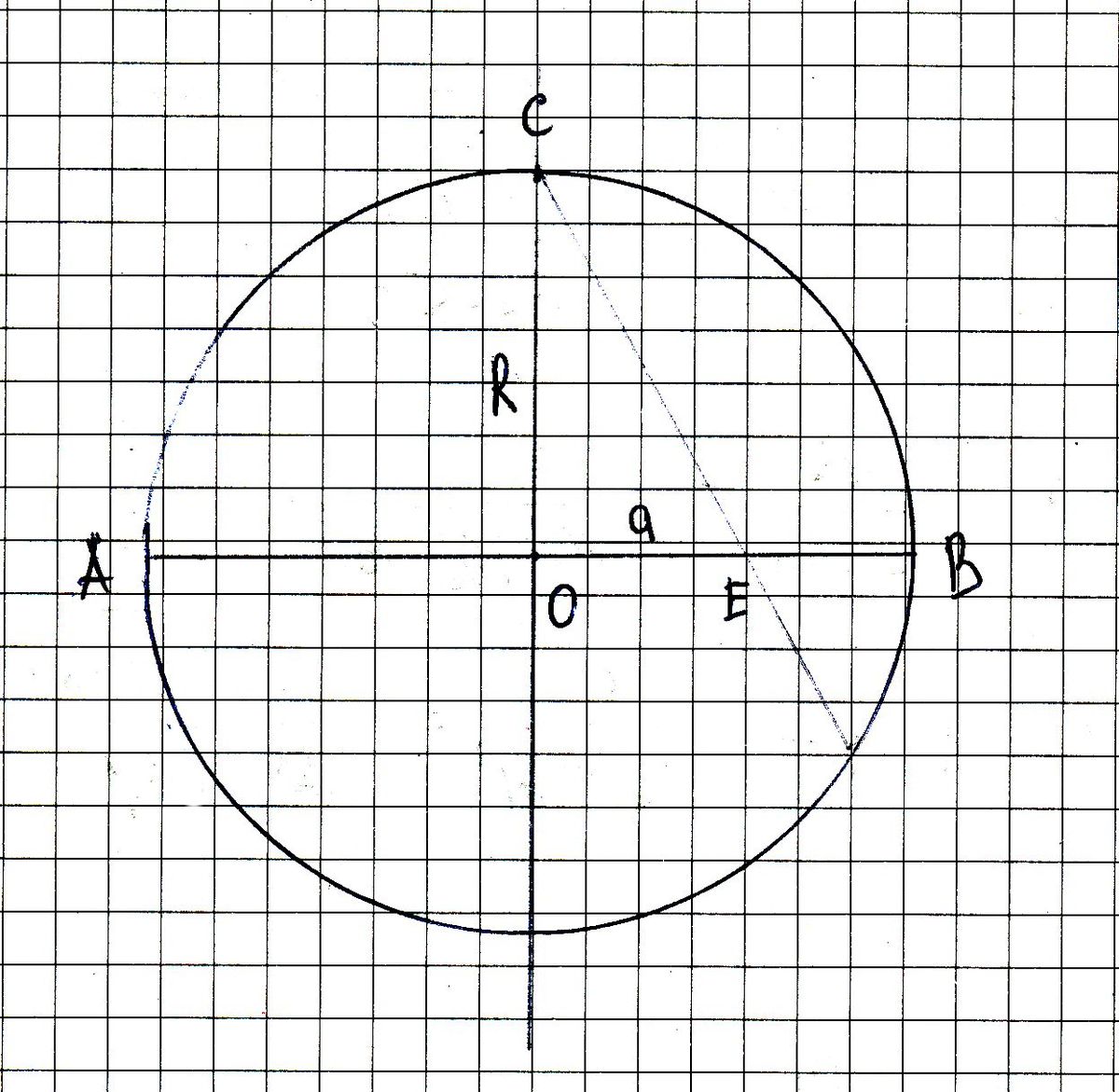
См. чертеж.
Прямые симметричны относительно ОС, поскольку усеченные круговые сегменты (один из них - СЕВ, ограничен дугой СВ) равны по площади, и оба равны четверти круга с вырезанным прямоугольным треугольником (справа это ОСЕ), следовательно, прямоугольные треугольники равны по площади, один катет у них общий, => они равны. Это - очевидно, но надо было это отметить.
Осталось понять, что 2*Scoe = Sceb = Socb - Scoe; :)
3*R*a/2 = pi*R^2/4;
ОЕ = а = pi*R/6; BE = R - a = R*(1 - pi/6);
Две прямые поделят диаметр на три отрезка
R*(1 - pi/6); pi*R/3; R*(1 - pi/6); ну, отсюда пропорция
(1 - pi/6) : (pi/3) : (1 - pi/6)