Question

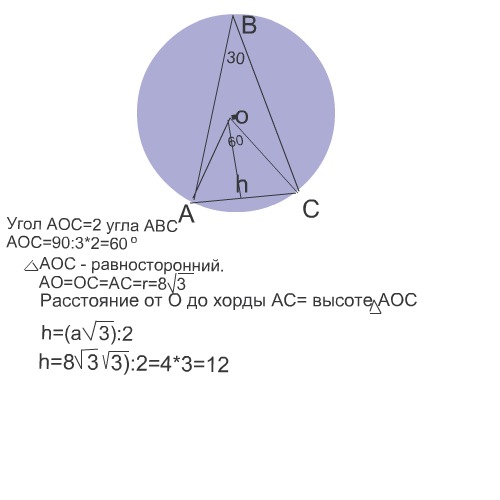
Сумма угла ABC вписанного в окружность и центрального угла AOC равна 90 грудусов. Найдите углы ABC и AOC и расстояние от центра окружности до хорды AC, если радиус окружности равен 8 корней из 3

 

 

P.S. Пожалуста при решении данной задачи пишите подробный ход решения!

Answer 1

Угол АВС равен половине дуги, на которую он опирается. Центральный угол АОС опирается на эту же дугу.  ∢АОС = ∢АВС*2

∢АОС + ∢АВС = 3 ∢ABC = 90 градусов

∢АВС = 30 градусов

∢АОС = 60 градусов

Треугольник АОС равнобедренный, углы при основании (180-60)/2=60, AC=R

ОD - высота тр-ка АОС,  расстояние от центра окружности до хорды AC

ОС = радиус R=8√3

DC = R/2 = 4√3

OD = √(8√3)²-(4√3)² = √(64*3-16*3)=12 

 

 

Answer 2

Угол АВС - вписанный и равен половние центрального АОС. 

Поэтому он равен 1/3 от 90 градусов и равен 30 градусов. 

Угол АОС=60 градусов. 

Треугольник АОС - равносторонний, т.к. угол при вершине О=60 градусов, углы при АС=60 градусов, т.к. АО=ОС.

Отсюда расстояние от О до АС= высоте равностороннего треугольника АОС.

Формула высоты равностороннего треугольника 

h=(а√3):2

h=(8√3*√3):2=12