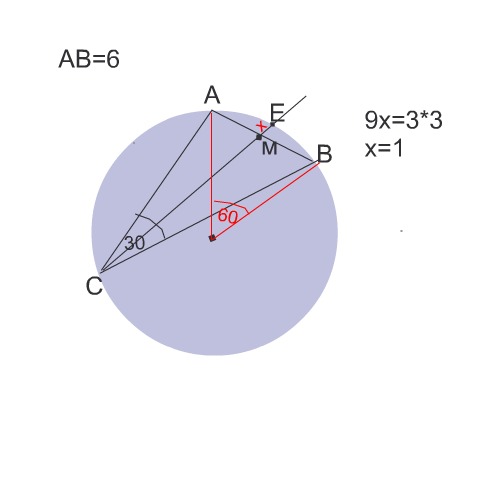
В окружности радиуса 6 см проведена хорда АВ. Через середину М этой хорды проходит прямая, пересекающая окружность в точках С и Е. Известно, что СМ = 9 см, <АСВ = 30°. Найдите длину отрезка СЕ.
Ответы
1) Пусть O - центр окружности, тогда центральный угол AOB=2*30=60 градусов (т.к. вписанный угол BCA=30 градусов)
2) Проведём OM - т.к. OM проходит в середину хорды, то OM перпендикулярно AB.
3) Рассмотрим треугольник AOB - OM высота равнобедренного треугольника, значит и биссектриса. Угол MOB=60/2=30 градусов.
4) Треугольник MOB - прямоугольный с гипотенузой 6 (OB - радиус), значит катет BM, лежащий против угла в 30 градусов равен половине гипотенузы, т.е. 6/2=3
5) Т.К. по условию MB=MA, то MA=3
6) Точка M внутренняя точка окружности, через неё проходят две пересекающиеся хорды, значит выполняется условие: BM*AM=EM*CM
7) с учётом вышенаписанного получим: 3*3=EM*9, отсюда EM=1.
8) CE=EM+MC=1+9=10 см
Делаем рисунок к задаче. Треугольник АВС находится полностью в одной половине окружности.
Соединим концы хорды АВ с центром окружности О. Получился равносторонний треугольник, так как центральный угол АОВ опирается на ту же дугу, на которую опирается вписанный угол АСВ, и поэтому угол АОВ равен 60 градусам.
Отсюда АВ=6 см.
Вспомним, что точкой пересечения хорды делятся на отрезки, произведения которых равны.
АЕ*ЕВ=СМ*МЕ.
Обозначим МЕ =х
3*3=9*х
х=1
МЕ=1
СЕ=9+1=10 см