Question

РЕШИТЕ НЕРАВЕНСТВО

 (x+5)(x-6) ≤0.

     6x-1

Answer 1

$frac{(x+5)(x-6)}{6x-1}geq0$

ОДЗ: R, кроме 6x-1=0

                          x=1/6

Представим в виде произведения:

$(x+5)(x-6)(6x-1)geq0$

Приравняем к нулю и найдём корни

(x+5)(x-6)(6x-1)=0

x=-5  x=6   x=1/6

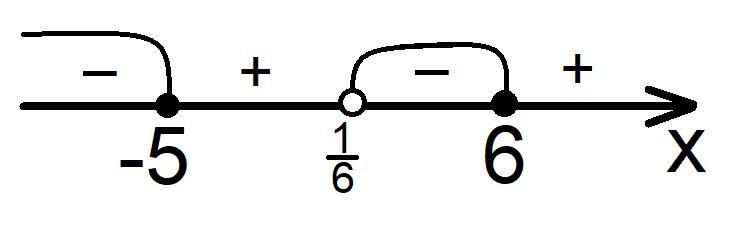
Отметим точки на координатной прямой, расставим знаки и запишем ответ

x = $(-infty;-5]cup(1/6; 6]$

Answer 2

$displaystyle frac{(x+5)(x-6)}{6x-1} le 0;quad frac{(x+5)(x-6)}{6bigg( x-dfrac16 bigg)} le 0quad bigg|cdot 6>0$

$displaystyle frac{(x+5)(x-6)}{x-frac16 } le 0$

Решим методом интервалов:

Отметим на координатной прямой точки, в которых знаменатель и числитель обращаются в ноль. У неравенства знак ≤ (а не <), поэтому закрашиваем точки из числителя. А точки из знаменателя, выкалываем т.к. на ноль делить нельзя в любом случаи. Мы разделили прямую на 4 интервала. На правом интервале ставим плюс т.к. перед дробью нету минуса. Далее через каждую точку чередуем знак т.к. чётных степеней нету. Нас интересует, когда меньше или равно нуля, поэтому выбираем интервалы с минусом и учитываем их границы.

$displaystyle xle -5; ; bigcup ; ; frac16 <xle 6$

Ответ: $displaystyle xin bigg( -infty ;-5bigg] bigcup bigg( frac16 ;6bigg] .$