Question

1)расстояние между скрещивающимися ребрами правильной треугольной пирамиды равно 12, а синус угла между боковым ребром и плоскостью основания равен 0,3. Найдите высоту основания пирамиды. 2)Тангенс угла между боковым ребром правильной четырехугольной пирамиды и плоскостью ее основания равен корень из 2. Найдите тангенс угла между плоскостью боковой грани и плоскостью основания пирамиды. 3)Высота основания правильной треугольной пирамиды равна 9, а высота боковой грани пирамиды, проведенная к ребру основания, равна корень из 73. Найдите боковое ребро пирамиды.

Answer 1

1)
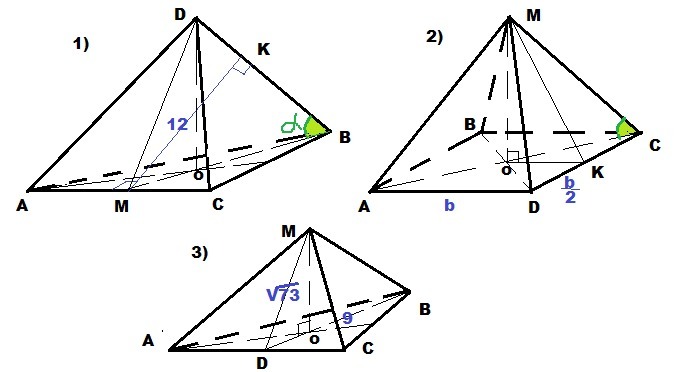
Правильная треугольная пирамида DABC
Расстояние между скрещивающимися прямыми DB и AC измеряется по их общему перпендикуляру KM
Прямая DB лежит в плоскости (MDB)⊥(ΔABC). 
DM⊥AC, DO⊥OM  ⇒  OM⊥AC   ⇒  BM⊥AC
BM - высота равностороннего треугольника основания.
ΔMKB: ∠MKB = 90°  ⇒
BM = MK / sin∠MBK = 12 / 0,3 = 40
Высота основания пирамиды равна 40.

 2)
Правильная четырёхугольная пирамида MABCD
tg∠MCO = √2
В основании пирамиды лежит квадрат ABCD со стороной b.
Высота пирамиды опускается в точку пересечения диагоналей квадрата.
Диагонали квадрата AC = BD = b√2
ΔMOC: ∠MOC = 90°   ⇒ 
OM = OC*tg∠MCO = (AC/2)* tg∠MCO = (b√2/2) * √2 = b
ΔMOK : ∠MOK = 90°   ⇒
tg∠MKO = OM / OK = b / (b/2) = 2
Тангенс угла между плоскостью боковой грани и плоскостью основания пирамиды равен 2

3)
Правильная треугольная пирамида MABC
В основании равносторонний ΔABC: BD = 9
Сторона основания 
AC = BD / sin60° = 9/(√3/2)=18/√3 = 6√3
Высота правильной пирамиды опускается в центр треугольника - точку пересечения медиан/высот/биссектрис.
Медианы треугольника делятся точкой пересечения в отношении 2:1 от вершины треугольника  ⇒  OD = BD/3 = 9/3 = 3;  OB = 6.
ΔMOD: ∠MOD = 90°; MO = √73; OD = 3  ⇒
OM² = (√73)² - 3² = 73 - 9 = 64 = 8²
ΔOMB: ∠MOB = 90°; OM = 8; OB = 6  ⇒
MB² = OM² + OB² = 8² + 6² = 100 = 10²
Боковое ребро равно 10