Предмет: Алгебра,
автор: shokoladka2195
Найдите наибольшее значение функции y= 4tgx-4x+П-7 на отрезке [-П/4; П/4].
Ответы
Автор ответа:
0
_____________________________
Решено при помощи использования формул:
( v + u )' = v' + u' — производная суммы
( tgx )' = 1/cos²x
ОТВЕТ: - 3
Решено при помощи использования формул:
( v + u )' = v' + u' — производная суммы
( tgx )' = 1/cos²x
ОТВЕТ: - 3
Приложения:
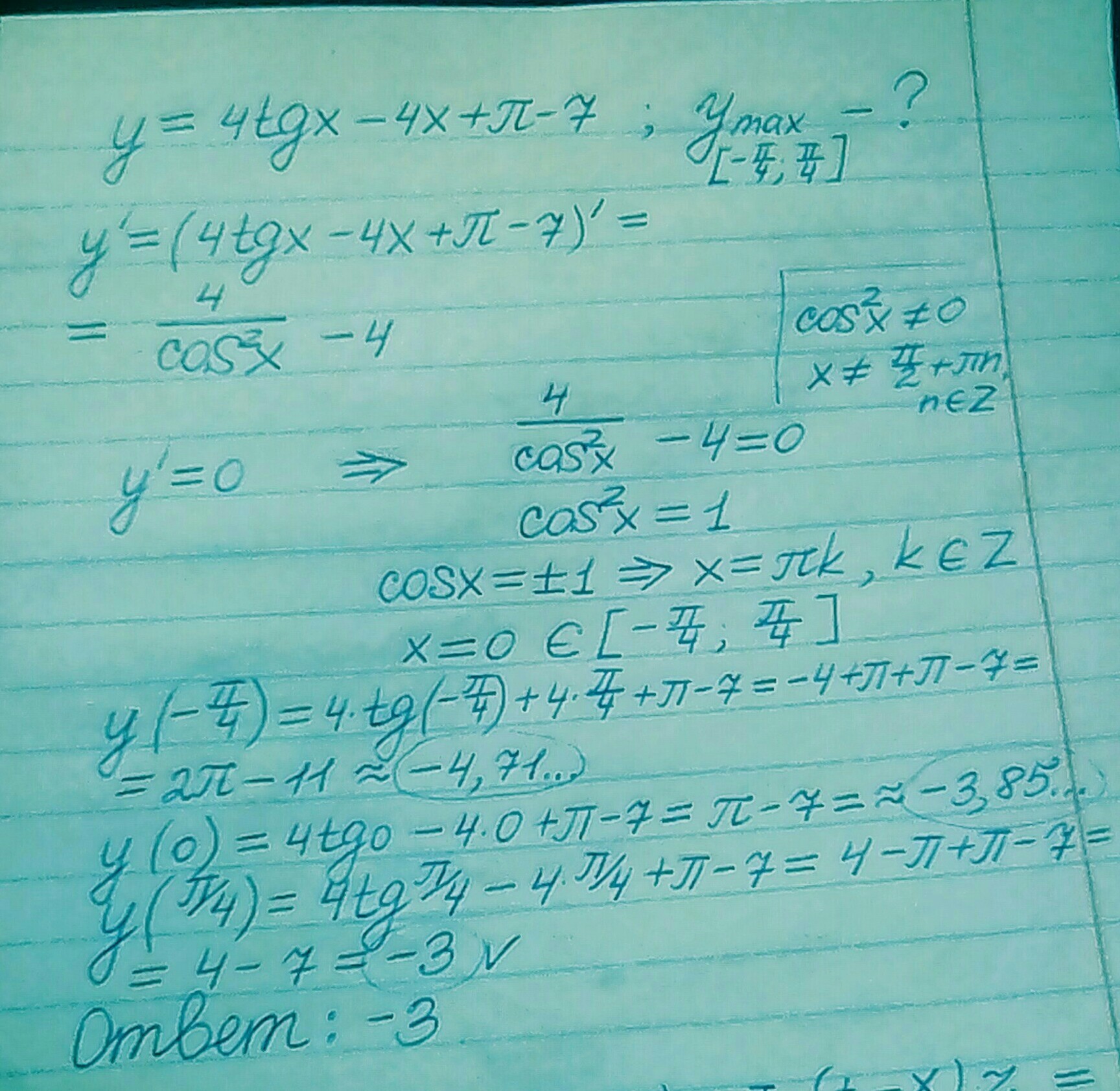
Автор ответа:
0
Найдем производную функцию:
Отберем корни принадлежащие отрезку [-π/4; π/4].
Если n=0, то x=0
Найдем наибольшее значение функции на концах отрезка:
Итак,
Приложения:
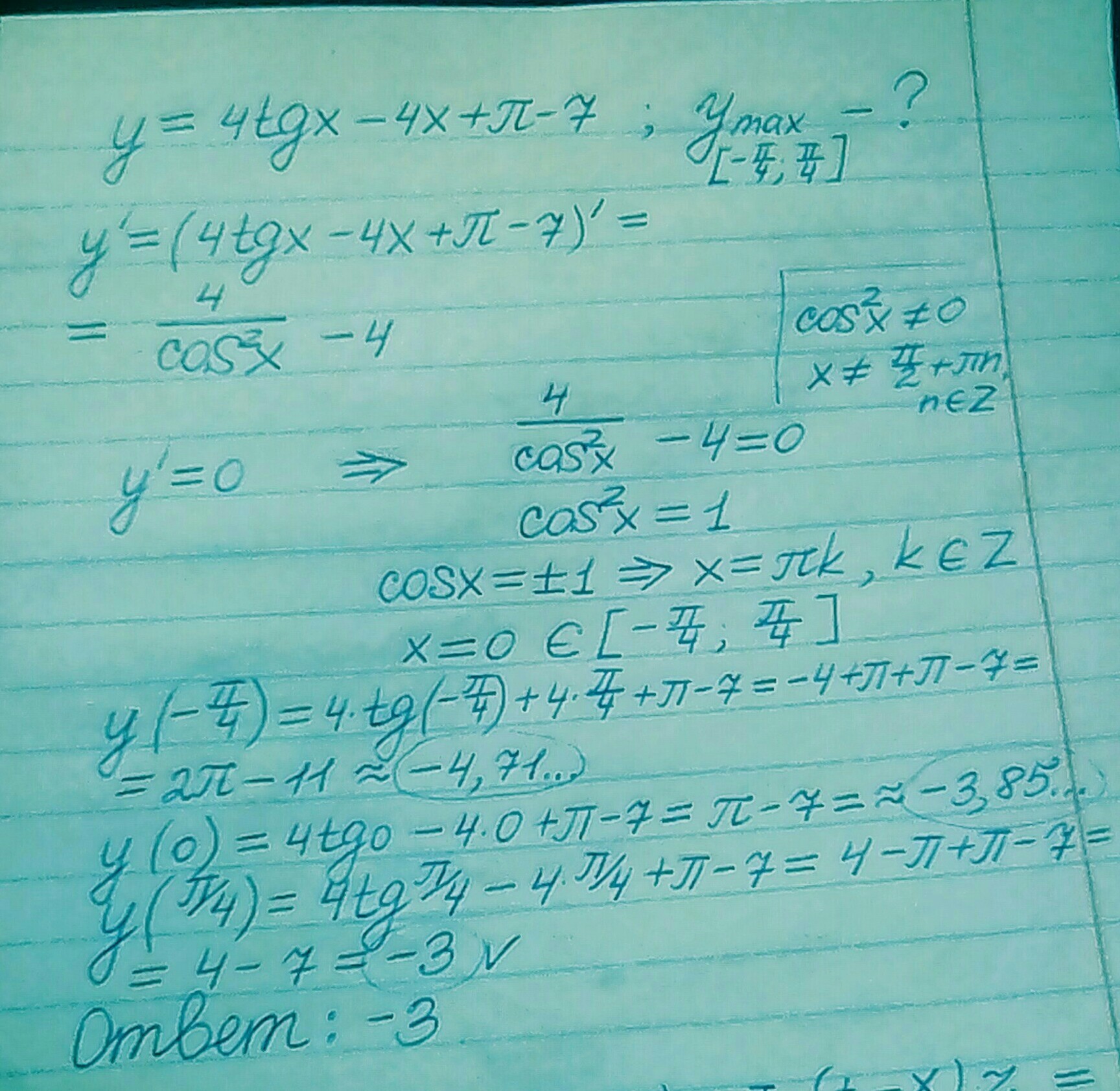
Похожие вопросы
Предмет: Математика,
автор: arina46kudva
Предмет: Алгебра,
автор: LaKrinze
Предмет: Алгебра,
автор: mila6447
Предмет: География,
автор: WillkaDilya
Предмет: Право,
автор: wwerow