Предмет: Алгебра,
автор: JuliaWoodsen
помогите пожалуйста решить с полным решением
Приложения:
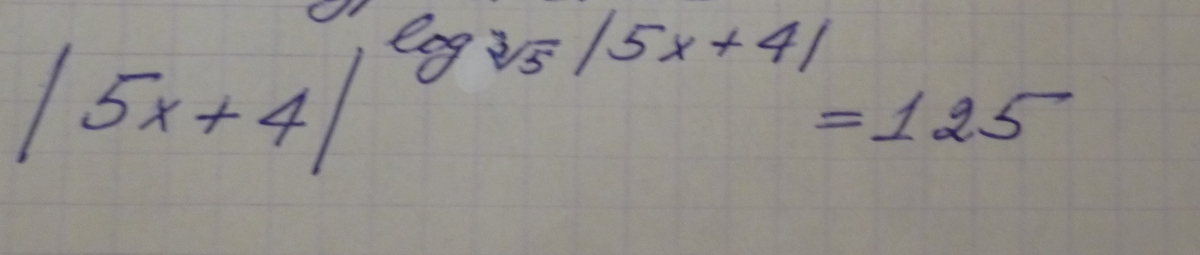
Ответы
Автор ответа:
0
|5x+4|>0,
[5x+4>0, -(5x+4)>0;
[x>-4/5, x<-4/5;
x≠-4/5;
[
[
[
[
[
[
[
[
[ 5x=-19/5, 5x=-21/5, 5x=1, 5x=-9;
[ x=-19/25, x=-21/25, x=1/5, 5x=-9/5;
Похожие вопросы
Предмет: Геометрия,
автор: dikaloroman8872
Предмет: Математика,
автор: icypai14
Предмет: Геометрия,
автор: luay82
Предмет: Информатика,
автор: Fizik98
Предмет: Литература,
автор: marina19800318