Question

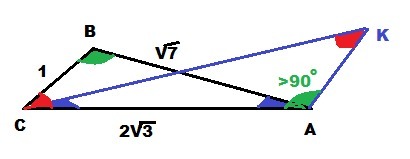
стороны АС АВ ВС треугольника АВС равны 2 корня из 3, корень из7 и 1 соответственно. точка К расположена вне треугольника АВС причем отрезок КС пересекает сторону АВ в точке, отличной от В. Известно что треугольник с вершинами К, А и С подобен исходному. Найдите косинус угла АКС, если угол КАС>90градусов

Answer 1

AC = 2√3;  AB=√7;  BC=1; ΔKAC~ΔABC;  ∠KAC > 90°

 ΔKAC~ΔABC;  ∠KAC > 90°  ⇒ против тупого угла в ΔKAC лежит самая большая сторона CK, а в подобном ему ΔABC самая большая сторона AC=2√3  ⇒  ∠ABC = ∠ KAC > 90°
∠KCA не может быть равен ∠ACB по построению  ⇒
∠KCA = ∠BAC;  ∠AKC = ∠ACB  ⇒
cos∠AKC = cos∠ACB

Теорема косинусов для ΔABC
AB² = AC² + CB² - 2AC*CB*cos∠ACB
√7² = (2√3)² + 1² - 2*2√3*1*cos∠ACB
7 = 13 - 4√3*cos∠ACB
4√3*cos∠ACB = 6
cos∠ACB = 6/(4√3)
cos∠ACB = √3/2   - табличный косинус  ∠ACB=30°

Ответ:   cos∠AKC = √3/2;  ∠AKC = 30°