Предмет: Геометрия,
автор: kamila091296
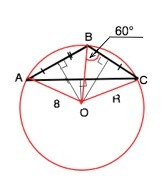
В остроугольном треугольнике АВС серединные перпендикуляры сторон АВ и АС пересекаются в точке О и ОА = 8. Найдите площадь треугольника ОВС, если угол ОВС = 60°.
Ответы
Автор ответа:
0
Точка пересечения серединных перпендикуляров треугольника - центр описанной вокруг него окружности.
Следовательно, ОВ=ОС=ОА=8 =R
В ∆ ВОС боковые стороны – радиусы, он – равнобедренный. ⇒
Углы при ВС равны, следовательно, все углы ∆ BOC равны 60°. ⇒
∆ ВОС - равносторонний. Площадь равностороннего треугольника находят по формуле
S (∆ ВОС)=64√3/4=16√3 (ед.площади).
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: mayanuraliyeva99
Предмет: История,
автор: berik030784
Предмет: Математика,
автор: kalugav063
Предмет: Математика,
автор: oleg099