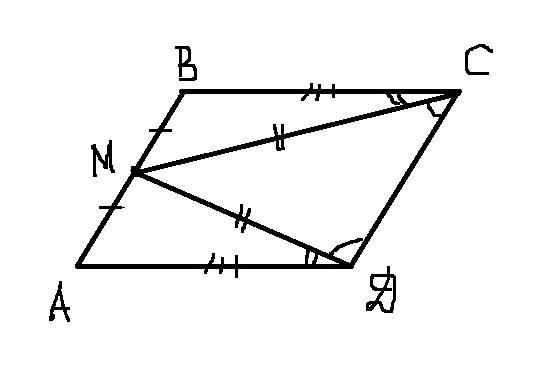
В параллелограмме АВСД точка М - середин стороны АВ. Известно, что МС=МД. Докажите, что данный параллелограмм - прямоугольник.
Ответы
треугольник DMC - равнобедренный, значит углы при основании равны угол MCD = угол MDC
треугольник MBC = треугольник AMD по трем сторонам (MC = MD, AM = MB, BC = AD)
тогда соответствующие углы равны угол ADM = угол BCM
т.е. угол BCD = угол ADC, следовательно ABCD - прямоугольник
Нарисуйте параллелограмм. Проведите в нем среднюю линию МН.
Соедините В и Н.
Теперь у вас есть параллелограмм МВСН, с диагоналями МС И ВН, а ВН=МД как равные диагонали в равных параллелограммах МВСН и АМНД.
Поэтому диагонали параллелограмма МВСН равны между собой по условию задачи.
Диагонали равны в параллелограмме, если он - прямоугольный. Параллелограмм АВСД - прямоугольник.
