Question

Основание АС равнобедренного треугольника АВС равно 18 см, а боковые стороны АВ и ВС равны 15 см. найдите радиусы вписанной и описанной около треугольника окружности. Помогите решить задачу только без этого : R = а·b·b/(4S) r = S/p

Answer 1

S=1/2 AC* h

найдём h 

высота в рванобедренном трегольнике- медиана 

AH=HC=9

H^2=15^2-9^2=144

H=12

S=108

P=48

r=2S/P

S=4.5

R=abc/4S

R=9

 

Answer 2

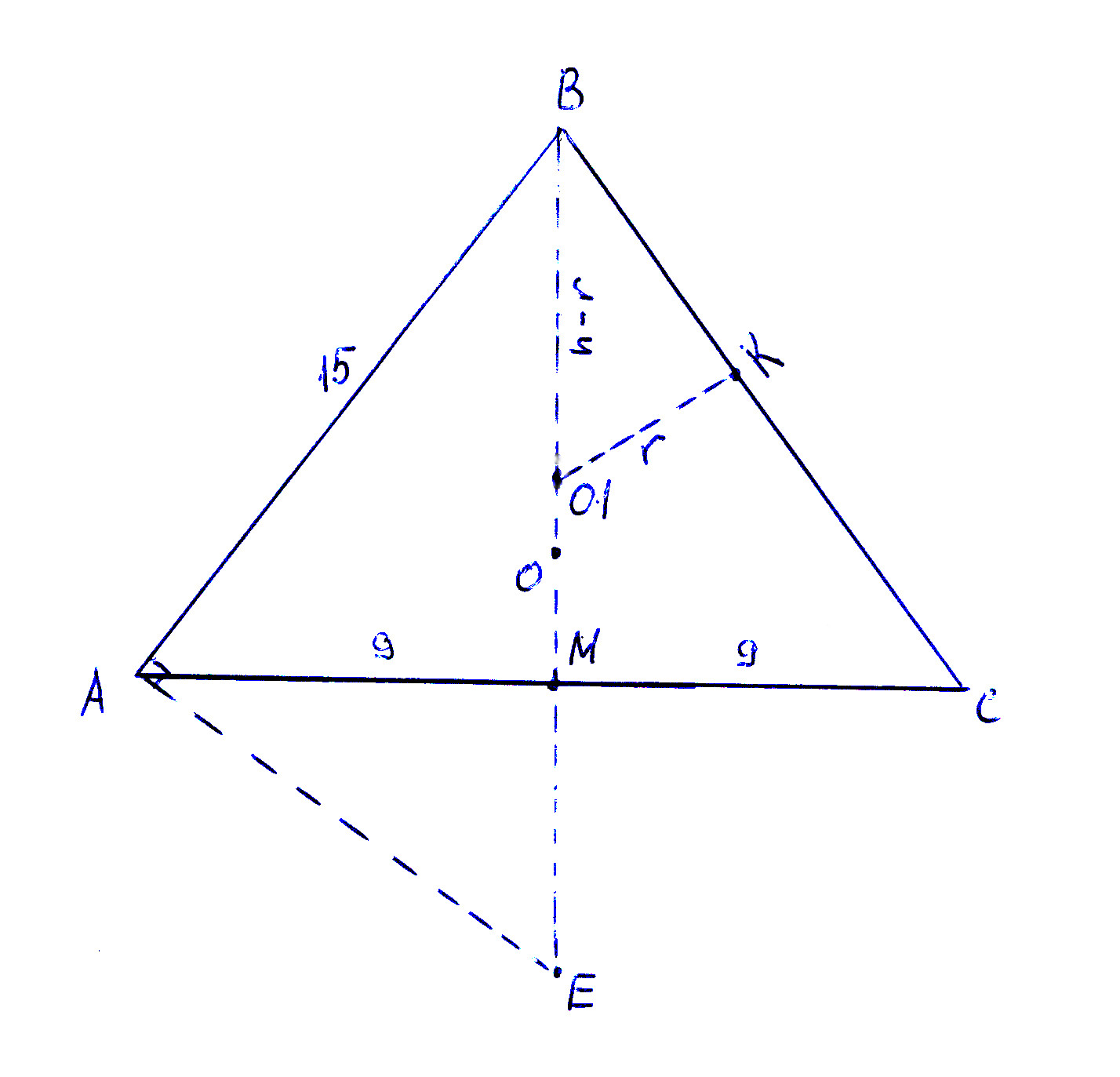
Да, без этих формул задача требует применения извилин :))) На чертеже представлены простые способы вычисления этих радиусов из простого подобия треугольников. Справа от высоты - способ вычисления радиуса вписанной окружности, в левой части риснка - радиуса описанной окружноти (точнее - диаметра:)).

Для начала следует понять, что АВС составлен из двух прямоугольных треугольников АВМ и ВМС, подобных "египетскому",  со сторонами 9, 12, 15. То есть высота ВМ = 12. 

1. О1 - центр вписанной окружности. О1К - радиус в точку касания. Из подобия треугольников ВМС и ВКО1 следует КО1/ВО1 = МС/ВС; при этом МО1 = КО1 = r;

r/(12 - r) = 3/5; r = 9/2;

2. Чтобы вычислить диаметр описанной окружности, для начала скажем, что центр её О лежит на ВМ. Продолжим ВМ до пересечения с описанной окружностью, пусть это точка Е (то есть ВЕ и есть диаметр D = 2*R). Тогда АЕ обязательно перпендикулярно АВ, так как вписанный в окружность угол ВАЕ опирается на диаметр ВЕ. Треугольники ЕАВ и АМВ прямоугольные и имеют общий угол АВМ. Поэтому они подобны, и ВЕ/АВ = АВ/ВМ. 

2*R/15 = 15/12, R = 75/8;