Question

Докажите что середины сторон ромба являются вершинами прямогольника 

Answer 1

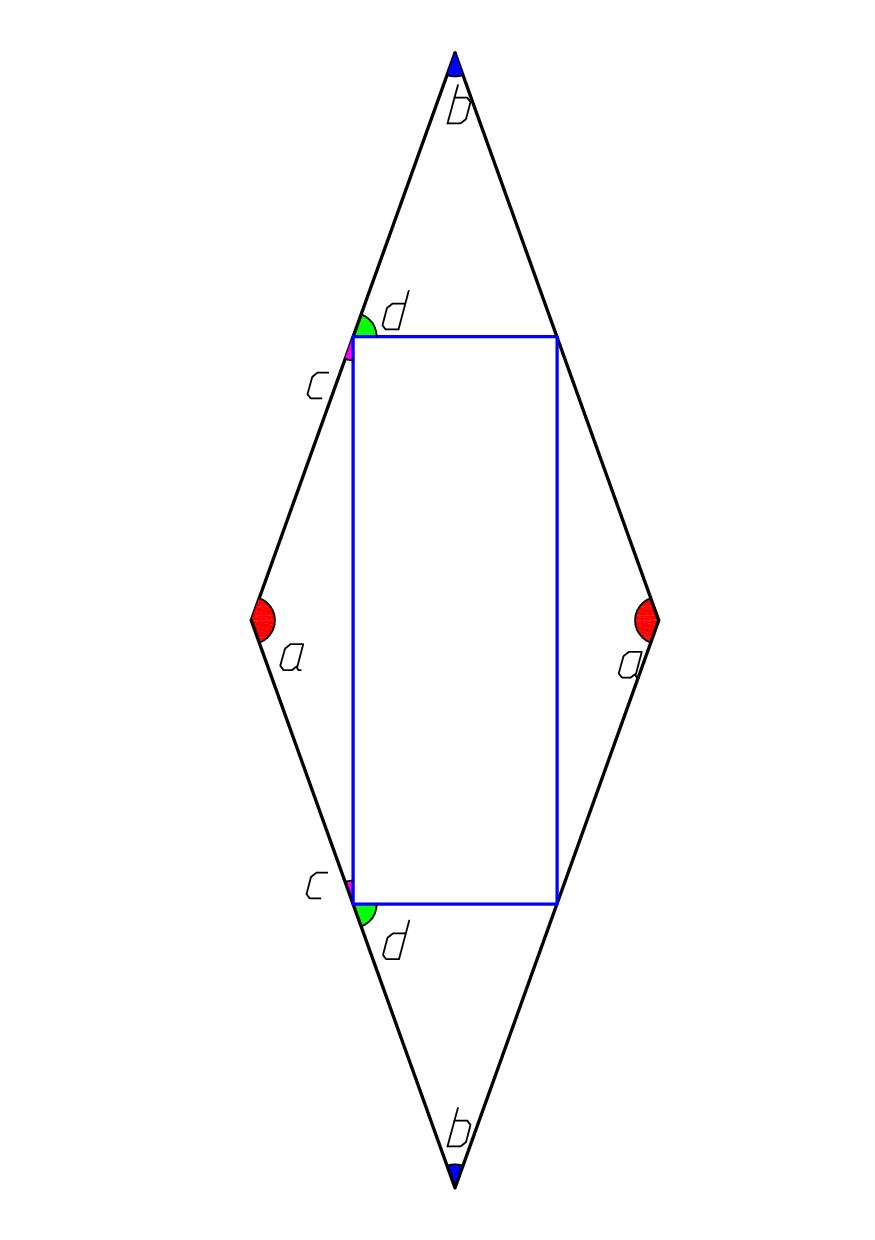
Рассмотрим ромб см.рис

В ромбе противоположные улы равны. Значит треугольники b-d и a-c равны соответственно. Отсюда противоположные стороны вписаного четырехугольника равны.

Эти треугольники ( b-d  и a-c) равнобедренные. Следовательно углы при катетах равны.

Теперь докажем что сумма углов c и d равна 90 град. 

Сумма углов ромба 2a+2b=360градусов или a+b=180

сумма углов в треугольнике b+2d=180 град и a+2c= 180град

выразим из последнего углы a и b

a=180-2c

b=180-2d

Подставим в первое уравнение

(180-2c)+(180-2d)=180

360-2c-2d=180 

360-180=2(c+d)

180/2=c+d

 c+d=90

Т.к развернутый угол равен 180 град, то оставшийся угол в четырехугольнике равен 180-(с+d)=90 град.

Значит вписан - прямоугольник.