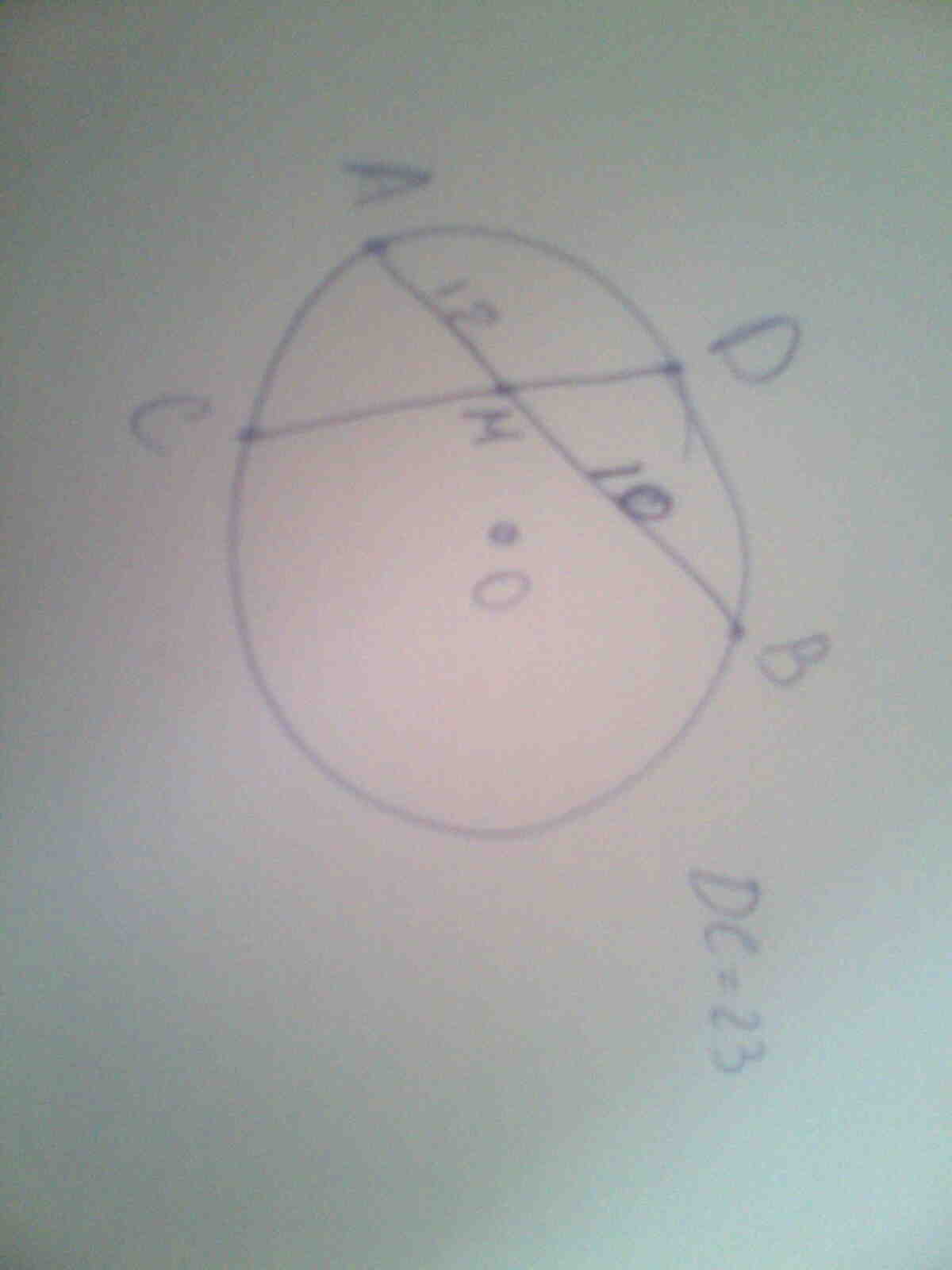
В окружности проведены 2 хорды AB и CD пересекающиеся в точке M, MB -10=см, AM=12см, DC= 23см Найдите длину CM и DM. ПОМОГИТЕ!
Ответы
так как в окружности проведены 2 хорды и они пересекаются в точке М, то АМ*МВ=СМ*МD
далее просто подставляем числа и получаем,что
12*10=СМ*МD=120
так как DC=23=CM+MD
пусть СМ = х см, тогда MD= 120/х
х+120/Х=23
(х^2+120)/х=23
23*х=х^2+120
решаем квадратичное уравнение через дискриминант
получаем что х1= 8, а Х2=15
если СМ=8, тогда MD=23-8= 15
Ответ:8 и 15
теорема:Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Исходя из этой теоремы мы получаем: АМ*МВ=СМ*СD
подставляем и находим, 12*10=СМ*СD
СМ*СD=120(1)
так как Dc=23 то мы DC можем представить как CM+DM=23
выражаем отсюда DM, DM=23-CM(2)
теперь второе выражение подставляем в первое:
CM*(23-CM)=120
120=23CM-CM²
CM²-23CM+120=0
решая квадратное уравнение мы получаем: CM=15 DM=8
не забудь сказать спасибо:*