Путешественник двигался от дома на запад и прошел 20 км, на следующий день он повернул на север и прошел еще 16 км, далее повернул на восток и прошел 8 км. На каком расстоянии (в км) от дома оказался путешественник?
Ответы
Пусть направление запад-восток - ось абсцисс (х), а направление север-юг - ось ординат(у). Координаты дома пусть будут (0;0) и он будет точкой отсчета.
В первый день путешественник пошел на запад на 20 км. Коорд. путешественника стали (-20;0), во 2 день он прошел на север 1 км и его коорд. - (-20;16)
А в третий день он пошел на восток на 8 км и его коорд. - (-12;16).
Если изобразить положение путешественника на листке, то получится прямоуг. треугольник со сторонами 12км и 16км. Пусть х - расстояние до дома. По теореме Пифагора:
х^2 = 12^2 + 16^2
х^2 = 144 + 256 (под корнем)
х^2 = 400
х = корень из 400.
х = в 20 км от дома оказался путешественник.
Ответ: в 20 км.
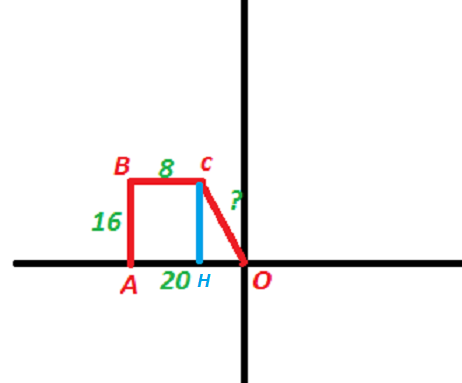
Начертим систему координат(смотри рисунок)
Из точки О вышел путешественник
он пошел на запад,то есть влево и остановился в точке А
Расстояние ОА=20км
Потом он повернул на север и прошел 16 км до точки В
Потом повернул на восток и прошел 8 км до точки С
Таким образом мы получили на системе координат отрезок ОС(он и будет расстоянием от дома до конечного пункта)
Четырехугольник АВСО трапеция,при чем трапеция прямоугольная,так как путешественник поворачивался на 90 градусов и угол ОАВ=90градусов
Нужно найти АО-боковую сторону трапеции
Проведем из точки В перпендикуляр к АО,тогда АН=8, НО=20-8=12
СН=АВ=16
Получили прямоугольный треугольник СНО,то по теореме Пифагора
ОС^2=CH^2+OH^2
OC^2=16*16+12*12=256+144=400
OC=20
Ответ:расстояние от дома до конечного пункта равно 20км.