Предмет: Алгебра,
автор: ТуПоЧкА55
Вычислите площадь фигуры, ограниченной линиями y=√-9x , y=3, x=0
Ответы
Автор ответа:
0
Найдем координаты точки пересечений линиями y=√-9x , y=3
3=√-9x
9=-9x
х=-1
(-1;3)
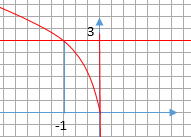
Делаем чертеж
Искомая площадь найдем как разность между площадью прямоугольника и криволинейной трапеции

3=√-9x
9=-9x
х=-1
(-1;3)
Делаем чертеж
Искомая площадь найдем как разность между площадью прямоугольника и криволинейной трапеции
Приложения:
Похожие вопросы
Предмет: Информатика,
автор: nilufar698
Предмет: История,
автор: djumashevasaikal
Предмет: Русский язык,
автор: DimaShutov
Предмет: Биология,
автор: chatte1