Question

одна из диагоналей прямоугольной трапеций делит этту трапецию на два прямоугольных равнобедренных треугольника.Какова площадь этой трапеций если ее меньшая боковая сторона равна 6?

Answer 1

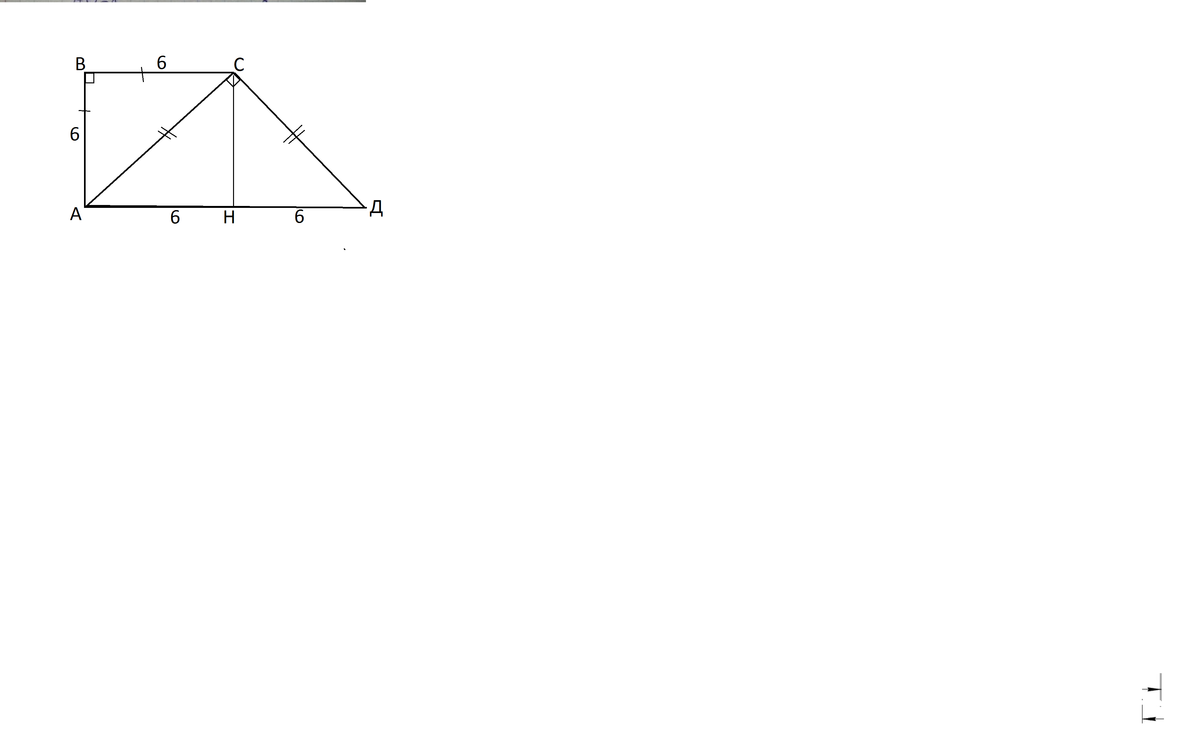
Пусть трапеция будет АВС, ВС и АД - основания.
Угол АВС =90°
АС- диагональ.  
Угол АСД =90°
Треугольник АВС - равнобедренный.
Следовательно, АВ=ВС=6
Высота СН отсекает от трапеции квадрат АВСН, и АН=6.
Треугольник АСД - равнобедренный.
АН=СН=6
АД=12
Площадь трапеции равна произведению высоты и полусуммы оснований:
S=СН*(ВС+АД):2= 6*18:2==54