Предмет: Алгебра,
автор: kirillsafronov
Решите это тоже, пожалуйста
Приложения:
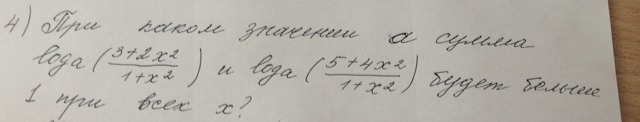
Ответы
Автор ответа:
0
С учетом
Получаем
Похожие вопросы
Предмет: Литература,
автор: anastaseml
Предмет: Литература,
автор: Аноним
Предмет: Алгебра,
автор: stepanbragin04
Предмет: Физика,
автор: anilegna
Предмет: Биология,
автор: fantom72