Question

Определите площадь боковой поверхности правильной четырехугольной пирамиды, если сторона основания равна (маленькой буквы) a и высота пирамиды равна h.

Answer 1

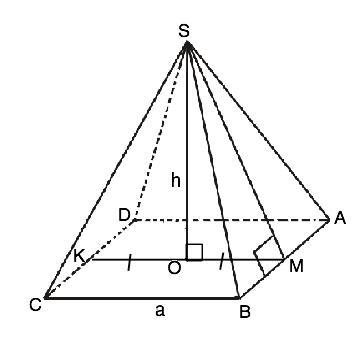
Ответ: Ѕ(бок)=a•√(4h²+a²)

Объяснение:

  В основании правильной четырехугольной пирамиды – квадрат,  боковые грани - равнобедренные треугольники, а вершина пирамиды проецируется в центр основания.

  Пусть данная пирамида SABCD,  SO - высота, ЅМ - апофема. КМ - средняя линия квадрата, КО=ОМ=а/2

  Площадь боковой поверхности пирамиды равна сумме площадей боковых граней. Ѕ(бок)=4•Ѕ(ASB)=4•BA•SM :2=2•BA •SM

SM=√(SO²+OM²)=√(h²+a²/4)=[√(4h²+a²)]:2

Ѕ(бок)=2•a•[√(4h²+a²)]:2= Ѕ(бок)=a•√(4h²+a²)